Cylinder: volume: CSA: TSA
Cylinder: Volume: CSA: TSA
One of the most commonly sighted geometric shapes is a cylinder where you can find it in fuel containers, gas tanks and even coffee mugs. The word ‘cylinder’ is derived from the Greek word, ‘kulindros’ which means a tumbler. In this chapter, you will be able to learn about cylinder and the capacity of the most used shapes.
Cylinder
A cylinder happens to be a close shape that has got two parallel bases which has a circular shape in general and is connected by two parallel sides. It is also defined as a rectangular that has rectangular bases. When it comes to the circular bases, it is always found to be parallel as well as congruent to one another. If cylinder is unrolled, then it gives a flattened look of a rectangle. A cylinder is formed by the base and sides. When the two circular bases joins the line at the center, it is known as the axis of the cylinder.
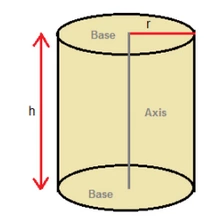
As seen in the figure above, height (h) happens to be the perpendicular distance between the two bases. Here, in each base has a radius (r.) Calculating the volume and surface area of the cylinder is possible from the measurement of height and radius.
Related Videos:
- Right Circular Cylinder
- Hemisphere: volume: CSA: TSA
- Cone: slant height: volume:CSA: TSA
- Frustum of a cone: formation and formulas ( slant height: volume: CSA: TSA)
Curved Surface Area
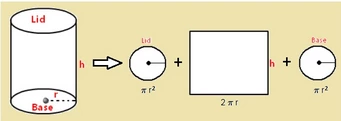
If you wish to calculate the curved surface of the geometrical figure, then the first thing to do is to take a sheet of paper and then wrap a cylindrical can. It is important to ensure that the paper is wrapped in such a way so that it accurately fits with this cylindrical can. You can also try to clip paper from bottom to top so as to match the shape of your can. The next thing that you need to do is to remove the paper and then cut the cylindrical paper where you need to make sure to cut it parallel to its axis and then make it rectangular in shape.
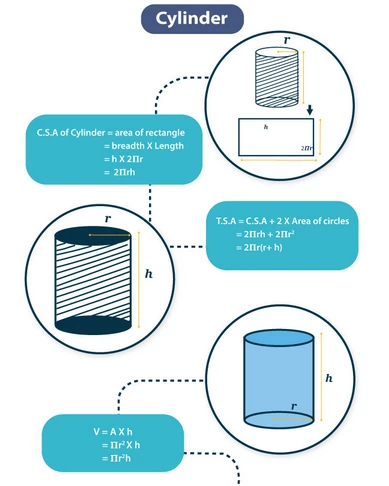
From the figure we find that the length of the cylinder = the circumference of the base = 2πr. h is the breadth of the rectangle = Height of the cylindrical can. As the rectangular paper was used in wrapping the Can, we have the knowledge that area of rectangle = area of the curved surface of the Cylindrical Vessel = l × b = 2πr × h
The Curved Surface Area of the Cylinder = 2πrh

Surface Area
We are quite familiar that the two bases joining the combination of rectangular like shape and two circular bases is the shape of a cylinder known as cylindrical shape. Therefore, when it comes to calculating the total surface area of the geometrical figure, it would include both the areas of the curved surface and the two bases. Therefore, we can find that the total surface area = Area of base 1 +Area of base 2+ Curved surface area
= πr2 +πr2 + 2πrh = 2πr2 + 2πrh = 2πr (r+h).
Thus,
The Surface Area of a Cylinder = 2πr (r+h)
Volume
The shape of the cylinder is built-up of a rectangle and that too with the same size. We can build a cylinder with the help of two circular bases. Now, in order to find the volume of this shape, it is important to consider a 3D counterpart of a rectangle called cuboid. By making use of the formula of the volume of a cuboid, the volume of any cylindrically shaped container can be charted out.
As we are quite familiar that the product of the area of a rectangle with height; l × b × h is the volume of the cuboid. So, you can find that the same situation is with a 3D cylindrical container. Here, in order to get the volume, it is important to take the product of the bases area and height. Thus we can find that area of circular base × height = πr2 × h which happens to be the volume of a cylindrical container.
The Volume of a Cylinder = πr2 h
Important Chapters:




Similar Questions
Knowledge Check
A cylinder is inscribed in a sphere of radius r
What is the radius of the cylinder of maximum volume ?A2r√3B√2√3rCrD√3r
Frustum of a cone: formation and formulas ( slant height: volume: CSA: TSA)
View SolutionWhen a stone is lowered into a measuring cylinder the volume is 9.3 ml. The volume of the stone is 5.8 ml. Find the initial volume of water in the measuring cylinder.
View SolutionLet the area of the base of a cylinder be B and the height of the cylinder be h. Write a formula for the cylinder’s volume V.
View SolutionVolume And Capacity|Volume Of Cuboid |Volume Of Cube|Volume Of Cylinder|Volume Of Cone|Volume Of Sphere|Volume Of Hemisphere|NCERT Example
View SolutionVolume And Capacity|Volume Of Cuboid|Volume Of Cube|Volume Of Cylinder|Volume Of Cone|Volume Of Sphere|Practice Problems
View SolutionSuppose you know the area of the base of a cylinder and the height of the cylinder. How can you find the cylinder’s volume?
View SolutionVolume Of Cylinder|Questions|Volume Of Cone|Questions|Volume Of Sphere|Questions|OMR
View Solution
