Sets and operations related to it
Sets and Operations
Sets, functions and relations all happen to be a part of the set theory. These tools help to carry out both mathematical and logical set operations on the different real-world entities. If there is a need to distinguish certain kind of objects in a group, then sets play a very important role in it. In the sets theory, you would be able to learn about the set as well as its properties. In this lesson, students would be able to learn about set laws and some important properties.
If ‘P’ is a set and ‘p’ happens to be one of its elements then P∈p denotes that the element ‘p’ belongs to ‘P.’ On the other hand, regarding ‘P∉p’, it means that ‘p’ is not an element of P. Therefore, it can be said that ‘P’ contains ‘p.’ So, it should be understood that a set is represented by capital letters, whereas small letter represents the element of the set.
Representation of Sets
In order to represent a set, there are mainly 3 ways for it:
- Statement form.
- Roaster form (tabular method).
- Set Builder form.
Statement Form
In this case, all the elements inside a set are described by a single statement. For example:
U = The set of all vowels in English
Roaster Form
In this form, a pair of braces {} which is separated by commas enlist all the members of the given set. Here, we can take an example:
The set of all odd numbers between 1 to 10:
O = {1, 3, 5, 7, 9}
Set Builder Form
In this case, a property is stated, which should prove to be common to all the elements that are present in a particular set. For example:
N = { x : x is positive integers between 10 to 20 }
Sets Formulas
Here, you can find some set formulas which are very important
n ( A ∪ B ) = n(A) + n(B) – n ( A ∩ B)
If A ∩ B = ∅, then n ( A ∪ B ) = n(A) + n(B)
n( A – B) + n( A ∩ B ) = n(A)
n( B – A) + n( A ∩ B ) = n(B)
n( A – B) + n ( A ∩ B) + n( B – A) = n ( A ∪ B )
n ( A ∪ B ∪ C ) = n(A) + n(B) + n(C) – n ( A ∩ B) – n ( B ∩ C) – n ( C ∩ A) + n ( A ∩ B ∩ C)
Types of Sets
Students need to be serious in getting the right knowledge on the types of sets as this can help to verify the proper set operations that are applicable to that particular set.
- Empty Set: Empty sets are those that do not contain any elements. These sets are also known as void sets or null sets which are denoted by {} or even Φ
- Equal Set: These sets contain identical elements where we can take an example like:
A = {3, 4, 5} and B = {3, 4, 8, 5, 7}.
Here, we can find that the elements of A and B are equal to each other (3, 4, 5) i. e., A = B
- Equivalent Sets: When you find that a particular set has got an equal number of members, it is called equivalent sets. For example:
A = {2, 5, 7) and B = { a, b, c}
Here, we can see that there are three elements in both A and B which are called equivalent sets.
- Finite and Infinite Sets: This is based on the number of finite or infinite elements which are present in the set. When it comes to infinite set, this is given as below:
N = Numbers divisible by 2 = {4, 6, 8, 10…..}
-
Singleton Set: Singleton set is a set that contains a single element. Here, for example, the number 9
-
Subsets: When the set of its elements also contains the set of elements of another set, then it is known as the subset. For example S = {4, 7}, R (S) = {{4,7}, {4}, {7}, {}} is the power set.
-
Super-sets: Here, in this type of set, the parent set contains all the elements of the subset, but at the same time, it may or may not contain extra elements.
S = The set of all colours and R = The set of all primary colours then, S ⊂ R; read as R is a “subset of” S or R is “contained in” S. Or we have:
S ⊃ R which means S is a “super-set of” R or S “contains” R.
Related Videos:
- Word problems related to operations of sets
- What is Set ?? Representation of set and Different type of sets
- Operations of Sets
Operations of Sets
Commutative Property :
A∪B = B∪A
A∩B = B∩A
Associative Property :
A ∪ ( B ∪ C) = ( A ∪ B) ∪ C
A ∩ ( B ∩ C) = ( A ∩ B) ∩ C
Distributive Property :
A ∪ ( B ∩ C) = ( A ∪ B) ∩ (A ∪ C)
A ∩ ( B ∪ C) = ( A ∩ B) ∪ ( A ∩ C)
Demorgan’s Law :
Law of union : ( A ∪ B )’ = A’ ∩ B’
Law of intersection : ( A ∩ B )’ = A’ ∪ B’
Complement Law :
A ∪ A’ = A’ ∪ A =U
A ∩ A’ = ∅
Idempotent Law And Law of null and universal set :
For any finite set A
A ∪ A = A
A ∩ A = A
∅’ = U
∅ = U’
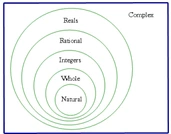
Let us consider the above figure, which is subsets of a set of complex numbers.
N = the set of natural numbers
W = the set of whole numbers.
I = the set of Integers.
Rt = the set of rational numbers.
Re = the set of real numbers.
C = the set of complex numbers.
Here, it can be said that N ⊂ W ⊂ I ⊂ Rt ⊂ Re ⊂ C. If we go in the reverse order, then we will get C ⊃ Re ⊃ Rt ⊃ I ⊃ W ⊃ N.
Important Chapters:
O = {1, 3, 5, 7, 9}
n ( A ∪ B ) = n(A) + n(B) – n ( A ∩ B)
If A ∩ B = ∅, then n ( A ∪ B ) = n(A) + n(B)
n( A – B) + n( A ∩ B ) = n(A)
n( B – A) + n( A ∩ B ) = n(B)
n( A – B) + n ( A ∩ B) + n( B – A) = n ( A ∪ B )
n ( A ∪ B ∪ C ) = n(A) + n(B) + n(C) – n ( A ∩ B) – n ( B ∩ C) – n ( C ∩ A) + n ( A ∩ B ∩ C)
Singleton Set: Singleton set is a set that contains a single element. Here, for example, the number 9
Subsets: When the set of its elements also contains the set of elements of another set, then it is known as the subset. For example S = {4, 7}, R (S) = {{4,7}, {4}, {7}, {}} is the power set.
Super-sets: Here, in this type of set, the parent set contains all the elements of the subset, but at the same time, it may or may not contain extra elements.
Commutative Property :
A∪B = B∪A
A∩B = B∩A
Associative Property :
A ∪ ( B ∪ C) = ( A ∪ B) ∪ C
A ∩ ( B ∩ C) = ( A ∩ B) ∩ C
Distributive Property :
A ∪ ( B ∩ C) = ( A ∪ B) ∩ (A ∪ C)
A ∩ ( B ∪ C) = ( A ∩ B) ∪ ( A ∩ C)
Demorgan’s Law :
Law of union : ( A ∪ B )’ = A’ ∩ B’
Law of intersection : ( A ∩ B )’ = A’ ∪ B’
Complement Law :
A ∪ A’ = A’ ∪ A =U
A ∩ A’ = ∅
Idempotent Law And Law of null and universal set :
For any finite set A
A ∪ A = A
A ∩ A = A
∅’ = U
∅ = U’

Similar Questions
Knowledge Check
- Question 1 - Select One
Operation Flood' is related to
Aflood controlBfish productionCmilk productionDgrain production - Question 2 - Select One
'Operation Flood' is related to
AFlood ControlBMilk ProductionCIrrigation DevelopmentDSoil Conservation - Question 3 - Select One
‘Machine’ is related to ‘Operator’ in the same way as ‘Car’ is related to ‘_________’
ABusBDriverCEngineDMechanic
On the set Q of all rational numbers an operation * is defined by a⋅b=1+ab. Show that * is a binary operation on Q.
View Solutionword problems related to operations of sets
View SolutionDefine identity element for a binary operation defined on a set.
View SolutionConsider the binary operation ∧on the set {1,2,3,4,5}defined by a∧b= min {a,b}. Write the operation table of the operation ∧.
View SolutionA relation in a set A is called ......... relation, if each element of A is related to itself.
View Solution

