Write the answer of each of the following questions:(i) What is the name of horizontal and the vertical lines drawn to determine the position of any point in the Cartesian plane?(ii) What is the name of each part of the plane formed by these two lines?(iii) Write the name of the point where these two lines intersect.
(i)The name of horizontal line drawn to determine the position of any point in the Cartesian plane is x-axis.
The name of vertical line drawn to determine the position of any point in the Cartesian plane is y-axis.
(ii)The name of each part of the plane formed by these two lines is quadrant. There are 4 quadrants in a cartesian plane.
(iii) Name of the point where these two lines intersect is origin.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
25 lines are drawn in a plane such that no two of them are parallel and no three of them are concurent. The number of points in which these lines intersect, is
A300B315C325D450 - Question 2 - Select One
25 lines are drawn in a plane. Such that no two of them are parallel and no three of them are concurrent. The number of points in which these lines intersect, is:
A300B315C325D450
Write 'T' for true and 'F' for false in case of each of the following statements
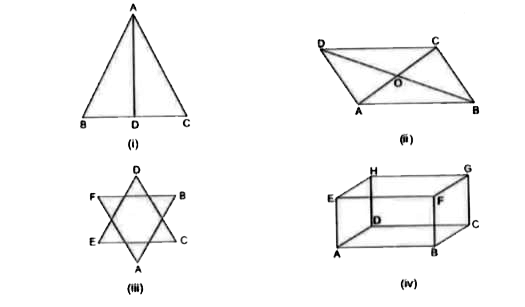
Two points A and B in a plane determine a unique line segment.View SolutionCount the number of line segments drawn in each of the following figures and name them.
 View Solution
View SolutionStudy the given figure and answer the following questions:
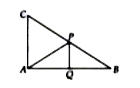
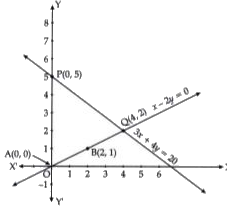
Name any two line segments inside the triangle ABC.View SolutionIf there are six straight lines in a plane, no two of which are parallel and no three of which pass through the same point, then find the number of points in which these lines intersect.
View SolutionShow that the locus of a point, equidistant from two intersecting lines in the plane, is a pair of lines bisecting the angles formed by the given lines.
View SolutionWrite 'T' for true and 'F' for false in case of each of the following statements
Two intersecting planes intersect at a point.View Solution