Write the coordinates of the points marked on the axes in Fig. 3.12.
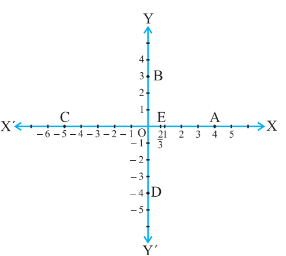
We can see the given graph that point A is at a distance of 3 units from the Y-axis and at a distance zero units from the X-axis.
Therefore the x-coordinate of A is 3 and y-coordinate is 0.
Hence, the coordinates of A are (3,0).
Similarly,
The coordinates of B are (2,0).
The coordinates of C are (−1,0).
The coordinates of D are (−2.5,0).
The coordinates of E are (−4,0).
So, as observed in figure, every point on the X-axis has 0 distance from X-axis.
Therefore the coordinate of a point lying on X-axis is always zero.
X-axis is denoted by the equation y=0.
Similar Questions
Knowledge Check
In Fig 4 the coordinates of point D are
A(b,a,0)B(a,b,0)C(b,c,0)D(0,b,c)
Locate the points A (1,2), B (4,2) and C (1,4) on a graph sheet taking suitable axes. Write the coordinates of the fourth point D to complete the rectangle ABCD.
View SolutionWrite the coordinates of the point dividing line segment joining points (2, 3) and (3, 4) internally in the ratio 1 :5 .
View SolutionThe coordinates of a point asre e(−5,−3,2). Write down the coordinates of seven points whose absolute values are the same as those of the coordinates of the given point.
View SolutionDraw the graph of line 4x+3y=24 Write the coordinates of points where this line intersects the x-axis and y-axis. Use this graph to find the area of the triangle formed by the line and the coordinates axes.
View SolutionThe coordinates of a point are (1,-2,7). Write down the coordinates of seven points, whose absolute values are the same as those of the coordinates of the given point.
View SolutionLocate the points A(1,2), B (3,4) and C (5,2) on a graph sheet taking suitable axes. Write the coordinates of the fourth point D to complete the rhombus ABCD. Measure the diagonals of this rhombus and find whether they are equal or not.
View SolutionIn fig. 28.7 if the coordinates of point P are (a,b,c) then Write the coordinates of points A, B, C, D, E and F. Write the coordinates of the feet of the perpendiculars from the point P to the coordinate axes. Write the coordinates of the feet of the perpendicular from the point P on the coordinate planes XY, YZ and ZX. Find the perpendicular distances of point P from XY,YZ and ZX− planes. Find the perpendicular distances of the point P fro the coordinate axes. Find the coordinates of the reflection of P are (a,b,c) . Therefore OA=a, OB=b nd OC=⋅
View Solution

