A, B, C are three non-zero matrices such that ABC = O, which of the following statements is true ?
|B|=0,|A|≠0,|C|≠0
|B|≠0,|C|=0,|A|≠0
|C|≠0,|B|≠0,|A|=0
none of these
The correct Answer is:D
To solve the problem, we need to analyze the given condition that the product of three non-zero matrices A, B, and C equals the zero matrix (O). We will also explore the implications of this condition on the determinants of these matrices.
1. Understanding the Condition:
We are given that ABC=O, where O is the zero matrix. This means that the product of matrices A, B, and C results in a matrix where all entries are zero.
2. Properties of Determinants:
Recall that for any square matrices A, B, and C, the determinant of the product of matrices is equal to the product of their determinants:
det(ABC)=det(A)⋅det(B)⋅det(C)
3. Applying the Condition:
Since ABC=O, we have:
det(ABC)=det(O)=0
Therefore, we can conclude that:
det(A)⋅det(B)⋅det(C)=0
4. Implication of the Determinant:
The product of the determinants being zero implies that at least one of the determinants must be zero. This means:
det(A)=0ordet(B)=0ordet(C)=0
Since A, B, and C are non-zero matrices, this means at least one of the matrices must be singular (not invertible).
5. Evaluating the Statements:
Now we need to evaluate the given statements:
- Statement 1: A=0
- Statement 2: B=0
- Statement 3: C=0
- Statement 4: None of these
Since we have established that at least one of the determinants must be zero, but we do not know which one, we cannot conclude that any specific matrix is zero. Therefore, the correct answer is that none of the statements can be definitively true.
Conclusion:
The correct statement is: None of these (Option 4).
---
We are given that ABC=O, where O is the zero matrix. This means that the product of matrices A, B, and C results in a matrix where all entries are zero.
Recall that for any square matrices A, B, and C, the determinant of the product of matrices is equal to the product of their determinants:
det(ABC)=det(A)⋅det(B)⋅det(C)
Since ABC=O, we have:
det(ABC)=det(O)=0
Therefore, we can conclude that:
det(A)⋅det(B)⋅det(C)=0
The product of the determinants being zero implies that at least one of the determinants must be zero. This means:
det(A)=0ordet(B)=0ordet(C)=0
Since A, B, and C are non-zero matrices, this means at least one of the matrices must be singular (not invertible).
Now we need to evaluate the given statements:
- Statement 1: A=0
- Statement 2: B=0
- Statement 3: C=0
- Statement 4: None of these
The correct statement is: None of these (Option 4).
Topper's Solved these Questions
- MATHEMATICS TIPSBook:FIITJEEChapter:MATHEMATICS TIPSExercise:ASSIGNMENT -OBJECTIVE
Explore 84 Videos
- MATHEMATICS TIPSBook:FIITJEEChapter:MATHEMATICS TIPSExercise:ASSERTION - REASONING
Explore 8 Videos
- MATHEMATICS TIPSBook:FIITJEEChapter:MATHEMATICS TIPSExercise:NUMERICAL DECIMAL BASED QUESTIONS
Explore 21 Videos
- MATHEMATICS Book:FIITJEEChapter:MATHEMATICS Exercise:NUMERICAL DECIMAL BASED QUESTIONS
Explore 15 Videos
- MATRICES Book:FIITJEEChapter:MATRICES Exercise:NUMERICAL BASED
Explore 3 Videos
Similar Questions
Knowledge Check
If →a,→b,→c are three non-zero vectors, then which of the following statement(s) is/are true?
A→a×(→b×→c),→b×(→c×→a),(→c×→a),→c×(→a×→b) form a right handed systemB→c,(→a×→b)×→c,→a×→b from a right handed systemC→a.→b+→b.→c+→c.→a<0 if →a+→b+→c=→0D(→a×→b).(→b×→c)(→b×→c).(→a×→c)=−1 if →a+→b+→c=0P is the incentre of Δ ABC. Which of the following statements is true ?
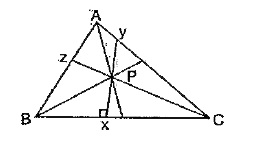 AAZ = BZBAY = BXCPY = PZDPA = PC
AAZ = BZBAY = BXCPY = PZDPA = PCLet a,b and c be three unit vectors such that 3a+4b+5c=0. Then which of the following statements is true?
Aa is parallel to bBa is perpendicular to bCa is neither parallel nor perpendicular to bDnone of these
If a,b and c be non-zero vectors, then which of the following statements is correct ?
View SolutionIf a, b and c are different integers such that a<b<c<o , then which of the following statements is true ?
View SolutionIf a, b, c be non-zero vectors, then which of the following statements are correct
View SolutionThe figure shows a nonconducting ring which has positive and begative charge non uniformly distributed on ot such that the total charfe is zero. Which of the following statements is true ?
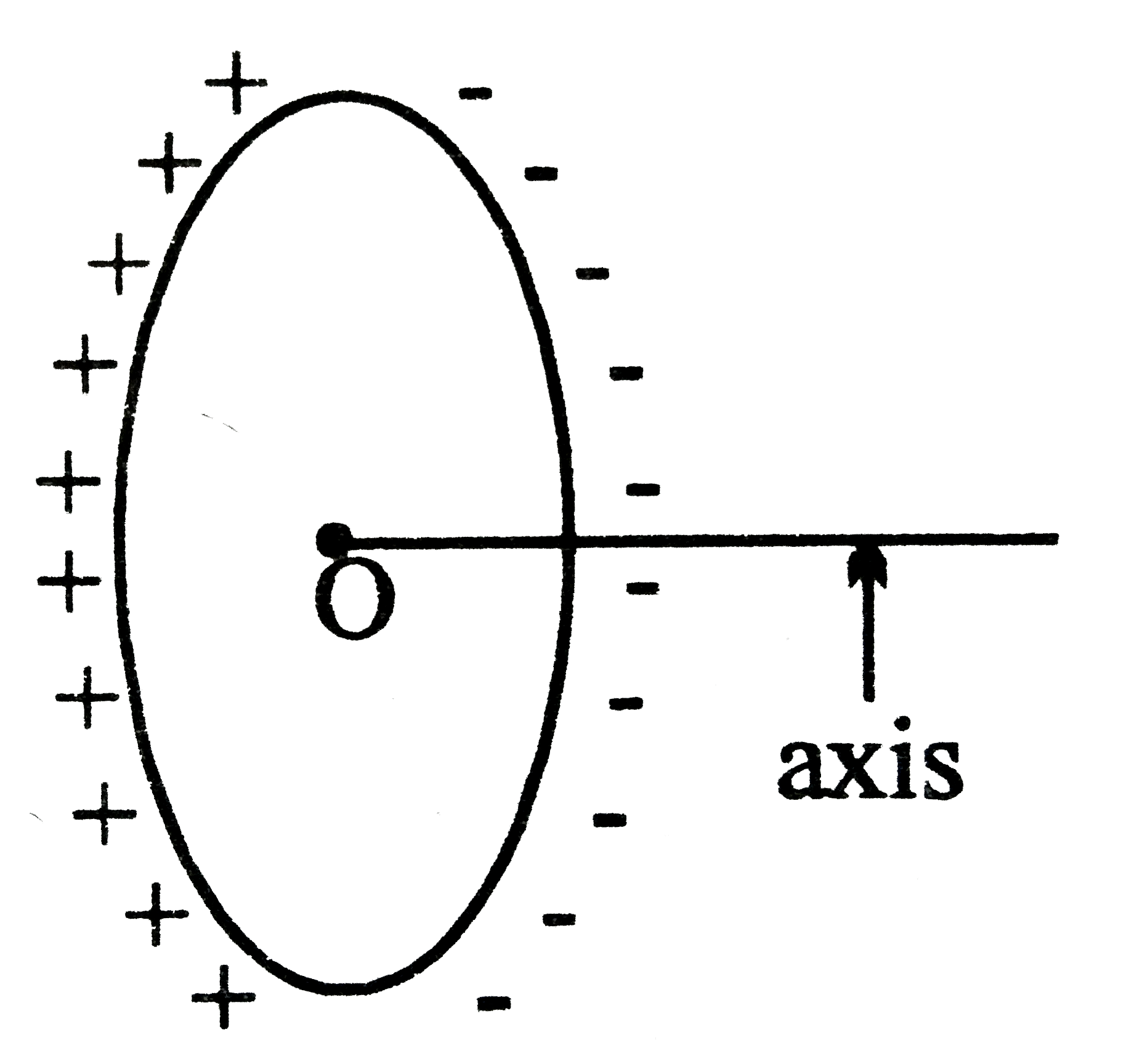 .
.
View SolutionLet a,b,c, are non-zero real numbers such that 1a,1b,1c are in arithmetic progression and a,b,−2c, are in geometric progression, then which of the following statements (s) is (are) must be true?
View Solution

