limx→1[cosecπx2]1/(1−x) (where [.] represents the greatest integer function) is equal to
The correct Answer is:1
Step by step video, text & image solution for underset(xto1)lim[cosec(pix)/(2)]^(1//(1-x)) (where [.] represents the greatest integer function) is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TIPSBOOK - FIITJEECHAPTER - TIPSEXERCISE - NUERICAL DECIMAL BASED QUATIONS
20 Videos
- TIPSBOOK - FIITJEECHAPTER - TIPSEXERCISE - PARAGRAPH BASED (MULTIPLE CHOICE) (COMPREHENSION - I)
39 Videos
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - MATHEMATICS
328 Videos
- TRIGNOMETRIC RATIOS AND IDENTITIESBOOK - FIITJEECHAPTER - TRIGNOMETRIC RATIOS AND IDENTITIESEXERCISE - All Questions
1 Videos
Similar Questions
Knowledge Check
limx→1[cosecπx2]1/(1−x) (where [.] represents the greatest integer function) is equal to
A0B1C∞DDoes not existslimx→0[(1−ex)sinx|x|] is (where [.] represents the greatest integer function )
A1B2C3Dnone of theselimx→1[x−1] where [] denotes the greatest integer function is equal to
A1B2C0DDoes not exist
To evaluate limx→a[f(x)], we must analyse the f(x) in right hand neighbourhood as well as in left hand neighbourhood of x=a. E.g. In case of continuous function, we may come across followign cases.

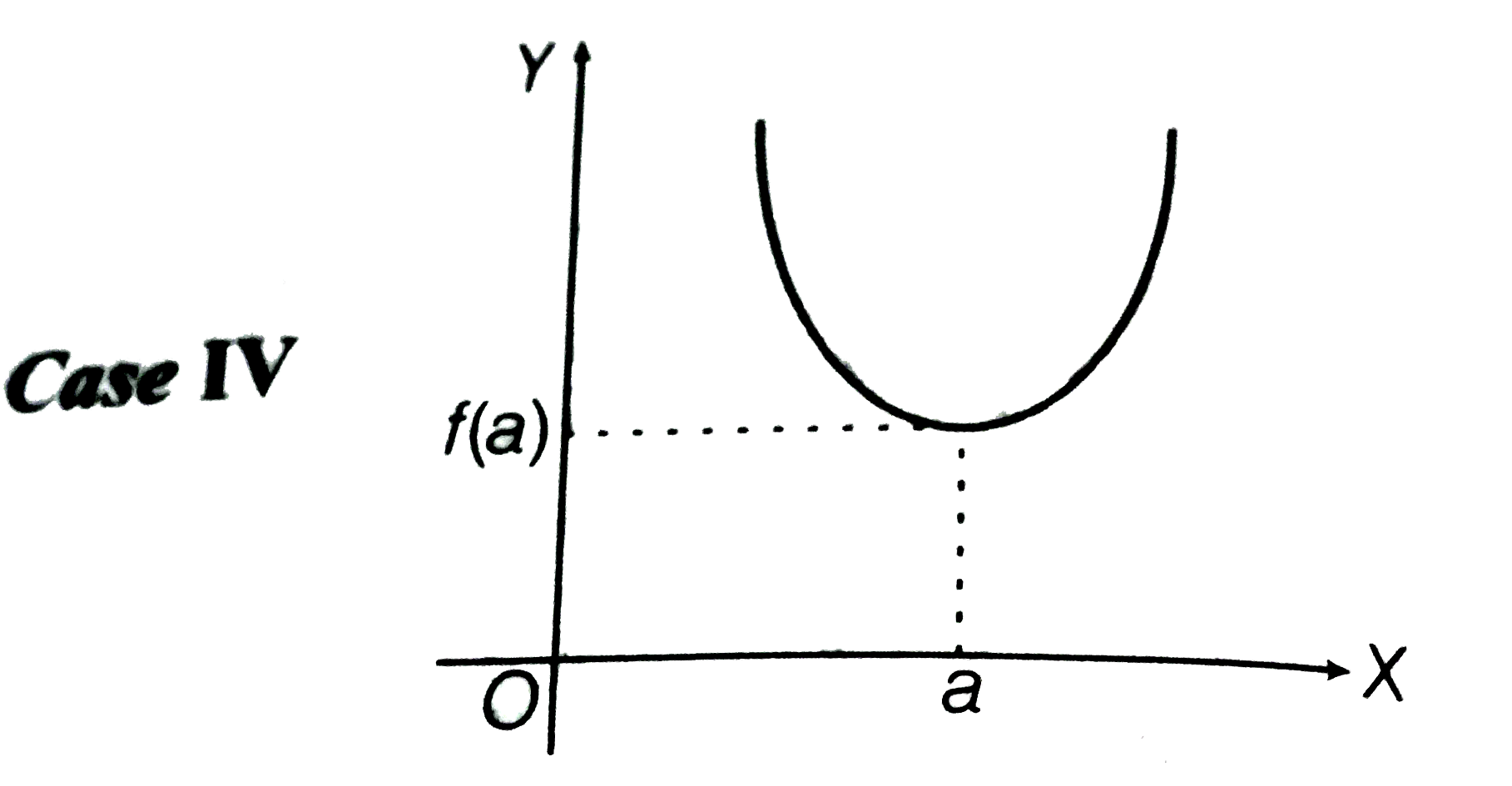
Iff(a) is an integer, the limit will exist in Case III and Case IV but not in Case I and Case II.limx→1[cosecπx2]−1/(1−x) is equal to (where [.] denotes the greatest integer function).
View Solutionlimx→0|x(x−1)|[cos2x], where [*] represents the greatest integer function, is equal to
View SolutionFind limx→0[x](e1/x−1e1/x+1), (where [.] represents the greatest integer funciton).
View Solutionlimx→0[sin(sgn(x))(sgn(x))], where [.] denotes the greatest integer function, is equal to
View Solution∫2−1[[x]1+x2]dx, where [.] denotes the greatest integer function, is equal to
View Solution
