A function is called one - one if each element of domain has a distinct image of co - domain or for any two or more the two elements of domain, function doesn't have same value. Otherwise function will be many - one. Function is called onto if co - domain = Range otherwise into. Function which is both one - one and onto, is called bijective. answer is defined only for bijective functions.
Let f:[a,∞)→[1,∞) be defined as f(x)=2x(x−1) be invertible, then the minimum value of a, is
0
1
1/2
none of these
The correct Answer is:B
To determine the minimum value of a such that the function f(x)=2x(x−1) is bijective from the domain (a,∞) to the range (1,∞), we need to ensure that the function is both one-to-one (injective) and onto (surjective).
1. Understanding the Function:
The function is given as f(x)=2x(x−1). This function is defined for x≥a and we want it to map to (1,∞).
2. Finding the Range of the Function:
- The expression x(x−1) is a quadratic function that opens upwards. It has its vertex at x=12.
- The value of x(x−1) at x=1 is 1(1−1)=0.
- For x<1, x(x−1)<0, and for x>1, x(x−1)>0.
- Therefore, f(x) will take the value f(1)=20=1 and will increase without bound as x increases beyond 1.
3. Ensuring the Function is One-to-One:
- To ensure that f(x) is one-to-one, we need to check the derivative f′(x).
- The derivative f′(x) can be found using the chain rule:
f′(x)=2x(x−1)⋅ln(2)⋅(2x−1)
- The function f′(x) will be positive when 2x−1>0 or x>12.
- Therefore, f(x) is increasing for x≥12.
4. Determining the Minimum Value of a:
- Since we want f(x) to be bijective, we need a to be at least 1 because f(1)=1 is the minimum value of the range.
- If a<1, then f(x) would not cover the entire range starting from 1.
5. Conclusion:
- The minimum value of a such that f(x) is bijective is a=1.
Final Answer:
The minimum value of a is 1.
The function is given as f(x)=2x(x−1). This function is defined for x≥a and we want it to map to (1,∞).
- The expression x(x−1) is a quadratic function that opens upwards. It has its vertex at x=12.
- The value of x(x−1) at x=1 is 1(1−1)=0.
- For x<1, x(x−1)<0, and for x>1, x(x−1)>0.
- Therefore, f(x) will take the value f(1)=20=1 and will increase without bound as x increases beyond 1.
- To ensure that f(x) is one-to-one, we need to check the derivative f′(x).
- The derivative f′(x) can be found using the chain rule:
f′(x)=2x(x−1)⋅ln(2)⋅(2x−1)
- The function f′(x) will be positive when 2x−1>0 or x>12.
- Therefore, f(x) is increasing for x≥12.
- Since we want f(x) to be bijective, we need a to be at least 1 because f(1)=1 is the minimum value of the range.
- If a<1, then f(x) would not cover the entire range starting from 1.
- The minimum value of a such that f(x) is bijective is a=1.
The minimum value of a is 1.
Topper's Solved these Questions
- TIPSBOOK - FIITJEECHAPTER - TIPSEXERCISE - NUMERICAL BASED QUESTIONS
23 Videos
- TIPSBOOK - FIITJEECHAPTER - TIPSEXERCISE - NUERICAL DECIMAL BASED QUATIONS
20 Videos
- TIPSBOOK - FIITJEECHAPTER - TIPSEXERCISE - MCQ (MULTIPLE CORRECT)
37 Videos
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - MATHEMATICS
328 Videos
- TRIGNOMETRIC RATIOS AND IDENTITIESBOOK - FIITJEECHAPTER - TRIGNOMETRIC RATIOS AND IDENTITIESEXERCISE - All Questions
1 Videos
Similar Questions
Knowledge Check
A function is called one - one if each element of domain has a distinct image of co - domain or for any two or more the two elements of domain, function doesn't have same value. Otherwise function will be many - one. Function is called onto if co - domain = Range otherwise into. Function which is both one - one and onto, is called bijective. answer is defined only for bijective functions.
If f:R→andf(x)=ax+sinx+a, thenAf(x) is one - one onto function if a∈RBf(x) is one - one onto function if a∈R−[−1,1]Cf(x) is one - one onto function if a∈R−{0}Df(x) is one - one onto function if a∈R−{−1}Function is said to be onto if range is same as co - domain otherwise it is into. Function is said to be one - one if for all x1≠x2⇒f(x1)≠f(x2) otherwise it is many one.
A function f:[0,∞) defined as f(x)=x1+x isAone - one and ontoBone - one but not ontoConto but not one - oneDneither one - one nor onto
Write the domain and range of the signum function,
View SolutionRange and domain of a functions

View SolutionDomain OF a function
View SolutionThe functions defined have domain R

View SolutionIn the given function, find the co-domain and range
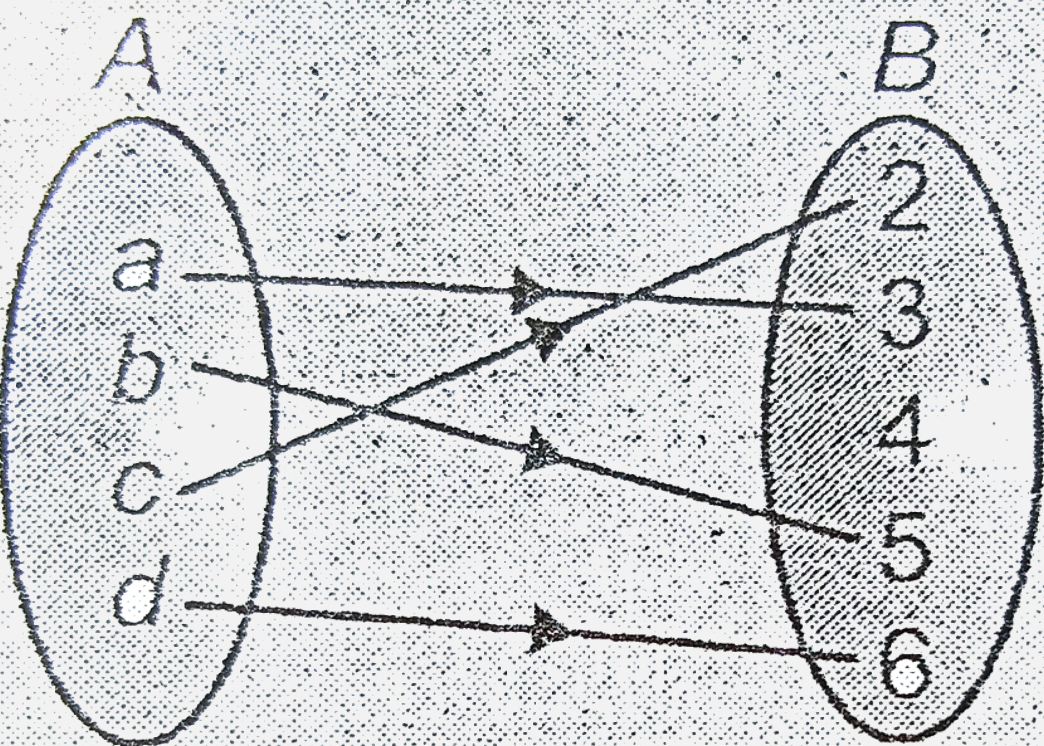
View SolutionIn the given function, find the domain, co-domain and range.
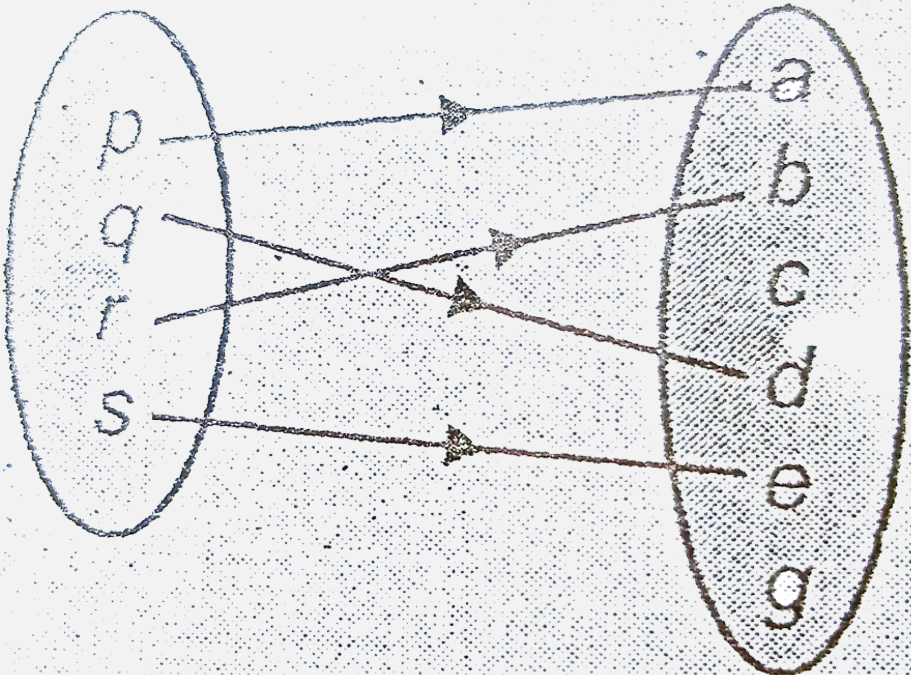
View Solution
