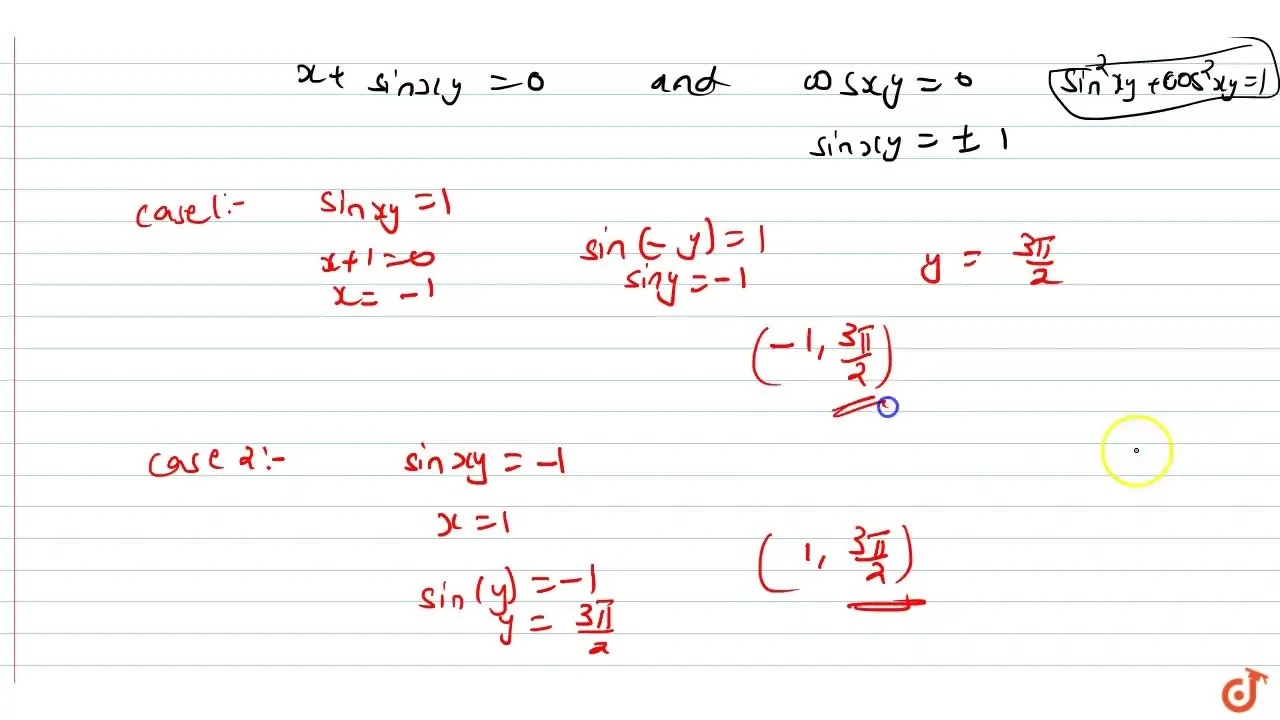The number of ordered pairs which satisfy the equation x2+2xsin(xy)+1=0 are (where y∈[0,2π] ) 1 (b) 2 (c) 3 (d) 0
The correct Answer is:x=±1y=2bπ−π2
Step by step video, text & image solution for The number of ordered pairs which satisfy the equation x^2+2xsin(x y)+1=0 are (where y in [0,2pi] ) 1 (b) 2 (c) 3 (d) 0 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - FIITJEECHAPTER - TRIGONOMETIC EQUATIONS EXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) (LEVEL 1) (FILL IN THE BLANKS )3videos
TRIGONOMETIC EQUATIONS
- BOOK - FIITJEECHAPTER - TRIGONOMETIC EQUATIONS EXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) (LEVEL II)16videos
TRIGONOMETIC EQUATIONS
- BOOK - FIITJEECHAPTER - TRIGONOMETIC EQUATIONS EXERCISE - EXERCISE5videos
TRIGONOMETIC EQUATIONS
- BOOK - FIITJEECHAPTER - TRIGNOMETRIC RATIOS AND IDENTITIESEXERCISE - All Questions1videos
TRIGNOMETRIC RATIOS AND IDENTITIES
- BOOK - FIITJEECHAPTER - VECTOREXERCISE - NUMERICAL BASED4videos
VECTOR
Similar Questions
The number of ordered pairs which satisfy the equation x2+2xsin(xy)+1=0 are (where y∈[0,2π] ) 1 (b) 2 (c) 3 (d) 0
View SolutionNumber of ordered pairs (x, y) which satisfies the relation x4+18x2=sin2y.cos2y where y∈[0,2π]
View SolutionNumber of ordered pairs (x, y) satisfying the equation 4y2+2cos2x=4y−sin2x, where x,y∈[0,2π], is
View SolutionThe number of ordered pairs of integers (x, y) satisfying the equation x2+6x+y2=4 is
View SolutionNumber of ordered pair (x,y) which satisfies the relation x4+18x2=sin2y⋅cos2y , where y∈[0,2π]
View SolutionNumber of ordered pairs (a, x) satisfying the equation sec2(a+2)x+a2−1=0;−π<x<π is
View SolutionNumber of ordered pair (x, y) satisfying x2+1=y and y2+1=x is
View SolutionThe number of ordered pair(s) (x. y) satisfying the equationssinx.cosy=1 and x2+y2≤9π2 is/are
View SolutionThe number of ordered pair(s) (x,y) of real numbers satisfying the equation 1+x2+2xsin(cos−1y)=0, is :
View SolutionTotal number of ordered pairs (x, y) satisfying |y|=cos x and y=sin−1(sinx) where x∈[0,3π] is equal to
View Solution