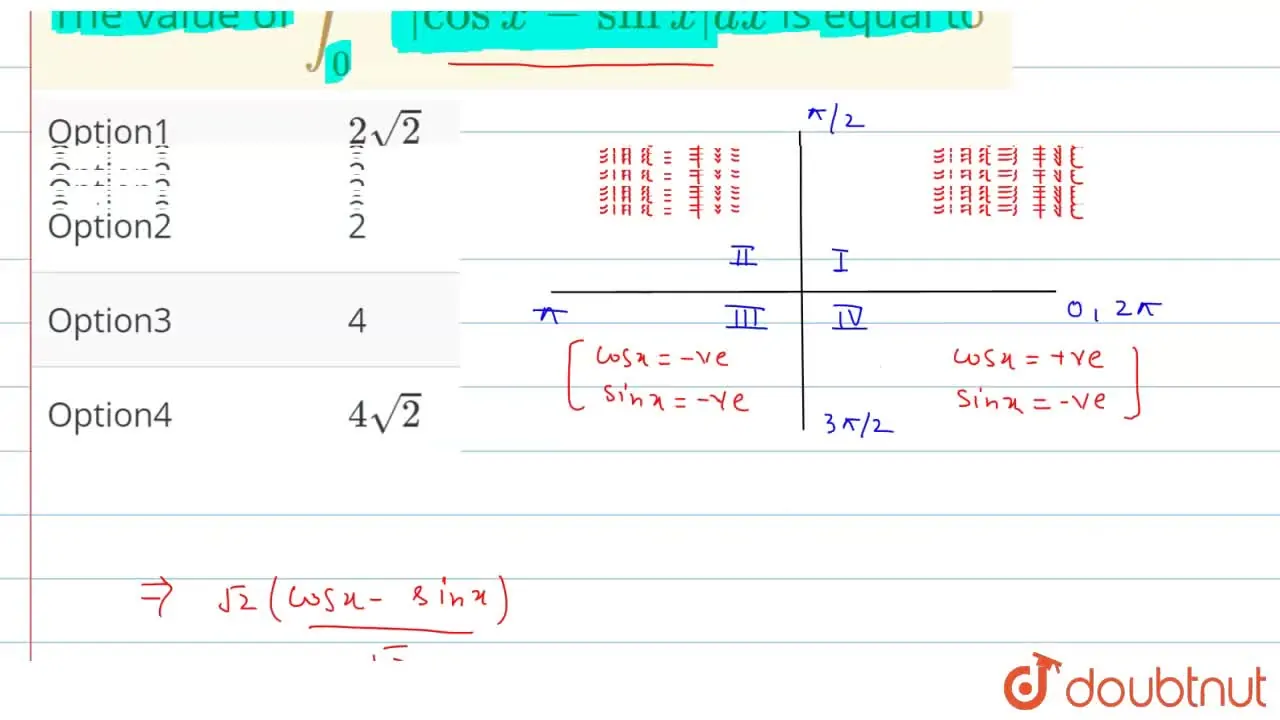
The value of ∫2π0|cosx−sinx|dx is equal to
A
2√2
B
2
C
4
D
4√2
Video Solution
|
Answer
Step by step video & image solution for The value of int_(0)^(2pi)|cosx-sinx|dx is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Related Playlists
- BOOK - FIITJEECHAPTER - DEFINITE INTEGRAL EXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) (LEVEL-II)15videos
DEFINITE INTEGRAL
- BOOK - FIITJEECHAPTER - DEFINITE INTEGRAL EXERCISE - COMPREHENSION I:3videos
DEFINITE INTEGRAL
- BOOK - FIITJEECHAPTER - DEFINITE INTEGRAL EXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) (LEVEL-II)10videos
DEFINITE INTEGRAL
- BOOK - FIITJEECHAPTER - COMPLEX NUMBEREXERCISE - NUMERICAL BASED3videos
COMPLEX NUMBER
- BOOK - FIITJEECHAPTER - DETERMINANTEXERCISE - NUMERICAL BASED3videos
DETERMINANT
Similar Questions
∫π20|sinx−cosx|dx is equal to
View Solution∫π/20cosx esinx dx is equal to
View Solution∫π/20cosx1+sinxdx is equal to
View SolutionThe value of ∫sinx−cosx√sin2xdx is equal to
View SolutionThe value of ∫π−πsinxf(cosx)dx is
View SolutionThe value of ∫π20sin2xsinx+cosxdx is equal to
View SolutionThe value of ∫π20sin2xsinx+cosxdx is equal to
View SolutionEvaluate ∫π/20|sinx−cosx|dx.
View SolutionThe value of ∫cos2x(sinx+cosx)2 dx is equal to
View SolutionThe value of the ∫sinx+cosx3+sin2xdx is equal to
View Solution