A conical vessel is to be prepared out of a circular sheet of gold of unit radius. How much sectorial area is to be removed from the sheet so that the vessel has maximum volume?
The correct Answer is:π(1−√23)
Step by step video, text & image solution for A conical vessel is to be prepared out of a circular sheet of gold of unit radius. How much sectorial area is to be removed from the sheet so that the vessel has maximum volume? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPLICATION OF DERIVATIVEBOOK - FIITJEECHAPTER - APPLICATION OF DERIVATIVEEXERCISE - SOLVED PROBLEMS (OBJECTIVE)
31 Videos
- APPLICATION OF DERIVATIVEBOOK - FIITJEECHAPTER - APPLICATION OF DERIVATIVEEXERCISE - Exercise 1
2 Videos
- APPLICATION OF DERIVATIVEBOOK - FIITJEECHAPTER - APPLICATION OF DERIVATIVEEXERCISE - Numerical
3 Videos
- AREABOOK - FIITJEECHAPTER - AREAEXERCISE - Numerical Based
3 Videos
Similar Questions
From a circular aluminium sheet of radius 14 cm, a sector of angle 45∘ is removed. Find the percentage of the area of the sector removed.
View SolutionFrom a circular aluminium sheet of radius 14 cm, a sector of angle 45∘ is removed. Find the percentage of the area of the sector removed.
View Solution
Knowledge Check
A conical vessel is to be prepared out of a circular sheet of metal of unit radius in order that the vessel has maximum value, the sectorial area that must be removed from the sheet is A1 and the area of the given sheet is A2, then A2A1 is equal to
A3+√6B7+√5C2+√5D3+√2A rectangular sheet of fixed perimeter with sides having their lengths in the ratio 8 : 15 is converted into an open rectangular box by folding after removing squares of equal area from all four corners. If the total area of removed squares is 100, the resulting box has maximum volume. The lengths of the sides of the rectangular sheet are :
A24B32C45D60A concave mirror of radius of curvature R has a circular outline of radius r. A circular disc is to be placed normal to the axis at the focus so that it collects all the light that is reflected from the mirror from a beam parallel to the axis. For r >>R, the area of this disc has to be at least
Aπr64R4Bπr44R2Cπr54R3Dπr4R2
A rectangular sheet of fixed perimeter with sides having their lengths in the ratio 8:15 is converted into anopen rectangular box by folding after removing squares of equal area from all four corners. If the total area of removed squares is 100, the resulting box has maximum volume. Then the length of the sides of the rectangular sheet are 24 (b) 32 (c) 45 (d) 60
View SolutionThere is an infinite non conducting sheet of charge having uniform charge density σ. The electric field at a point P at a distance x from the sheet is E0. Point O is the foot of the perpendicular drawn from point P on the sheet. A circular portio of radius r<<x centered at O is removed from the sheet. Now the field at point P becomes E0−ΔE. Find ΔE.
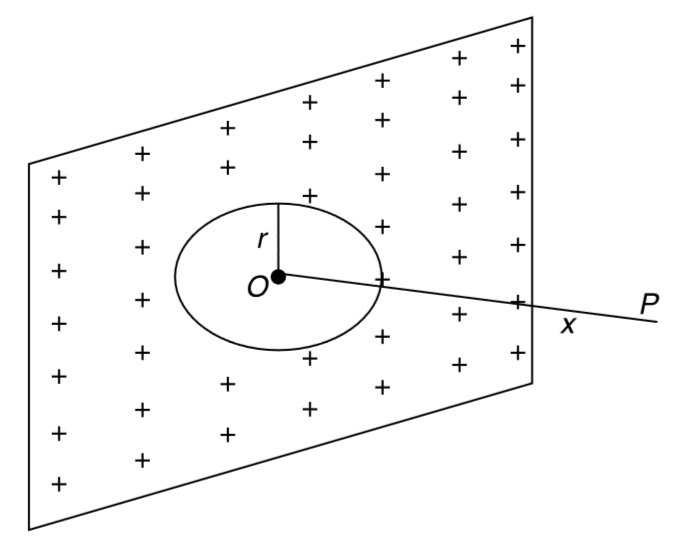
View SolutionA square sheet of maximum area is cut out from a circular piece of carboard of radius 21 cm. Find the area of the remaining card board.
View SolutionIt takes 13.5 mL to paint the surface of the circular sheet of radius 17 cm . How much paint is required to paint a similar circular sheet with double the radius ?
View SolutionA rectangular sheet of fixed perimeter with sides having their lengths in the ratio 8:15 is converted into an open rectangular box by folding after removing squares of equal area from all four corners if the total area of removed squares is 100 the resulting box has maximum volume the lengths of the sides of the rectangular sheet are
View Solution
