Calculate the median deviation from the median of the following data: Wages per week (in Rs.), 10-20, 20-30, 30-40, 40-50, 50-60, 60-70, 70-80 No. of workers, 4, 6, 10, 20, 10, 6, 4
To calculate the median deviation from the median of the given data, follow these steps:
Step 1: Create a frequency distribution table
We have the following data:
| Wages per week (in Rs.) | No. of workers (Frequency) |
|--------------------------|---------------------------|
| 10-20 | 4 |
| 20-30 | 6 |
| 30-40 | 10 |
| 40-50 | 20 |
| 50-60 | 10 |
| 60-70 | 6 |
| 70-80 | 4 |
Step 2: Calculate the mid-point (X_i) for each class interval
The mid-point for each class interval is calculated as follows:
- For 10-20: (10 + 20)/2 = 15
- For 20-30: (20 + 30)/2 = 25
- For 30-40: (30 + 40)/2 = 35
- For 40-50: (40 + 50)/2 = 45
- For 50-60: (50 + 60)/2 = 55
- For 60-70: (60 + 70)/2 = 65
- For 70-80: (70 + 80)/2 = 75
Now, we add these mid-points to our table:
| Wages per week (in Rs.) | No. of workers (Frequency) | Mid-point (X_i) |
|--------------------------|---------------------------|------------------|
| 10-20 | 4 | 15 |
| 20-30 | 6 | 25 |
| 30-40 | 10 | 35 |
| 40-50 | 20 | 45 |
| 50-60 | 10 | 55 |
| 60-70 | 6 | 65 |
| 70-80 | 4 | 75 |
Step 3: Calculate the cumulative frequency
Now, we calculate the cumulative frequency (CF):
| Wages per week (in Rs.) | No. of workers (Frequency) | Cumulative Frequency (CF) |
|--------------------------|---------------------------|---------------------------|
| 10-20 | 4 | 4 |
| 20-30 | 6 | 10 |
| 30-40 | 10 | 20 |
| 40-50 | 20 | 40 |
| 50-60 | 10 | 50 |
| 60-70 | 6 | 56 |
| 70-80 | 4 | 60 |
Step 4: Determine the median class
The total number of workers (N) is 60. To find the median class, we calculate N/2 = 60/2 = 30. The cumulative frequency just greater than 30 is 40, which corresponds to the class interval 40-50. Therefore, the median class is 40-50.
Step 5: Calculate the median using the formula
Using the median formula:
Median=l+(N/2−Ff)×h
Where:
- l = lower boundary of the median class = 40
- N = total frequency = 60
- F = cumulative frequency of the class before the median class = 20
- f = frequency of the median class = 20
- h = width of the median class = 10
Plugging in the values:
Median=40+(30−2020)×10=40+(1020)×10=40+5=45
Step 6: Calculate the deviation from the median
Now, we calculate the deviation di for each class:
di=Xi−Median
| Mid-point (X_i) | Deviation (d_i) |
|------------------|-----------------|
| 15 | 15 - 45 = -30 |
| 25 | 25 - 45 = -20 |
| 35 | 35 - 45 = -10 |
| 45 | 45 - 45 = 0 |
| 55 | 55 - 45 = 10 |
| 65 | 65 - 45 = 20 |
| 75 | 75 - 45 = 30 |
Step 7: Calculate the absolute deviation
Now we take the absolute values of the deviations:
| Mid-point (X_i) | Absolute Deviation (|d_i|) |
|------------------|----------------------|
| 15 | 30 |
| 25 | 20 |
| 35 | 10 |
| 45 | 0 |
| 55 | 10 |
| 65 | 20 |
| 75 | 30 |
Step 8: Calculate fi×|di|
Now, we multiply the absolute deviations by their respective frequencies:
| Mid-point (X_i) | Frequency (f_i) | |d_i| | fi×|di| |
|------------------|-----------------|------|-------------------|
| 15 | 4 | 30 | 120 |
| 25 | 6 | 20 | 120 |
| 35 | 10 | 10 | 100 |
| 45 | 20 | 0 | 0 |
| 55 | 10 | 10 | 100 |
| 65 | 6 | 20 | 120 |
| 75 | 4 | 30 | 120 |
Step 9: Calculate the sum of fi×|di|
Now, we sum up the last column:
Σfi|di|=120+120+100+0+100+120+120=680
Step 10: Calculate the mean deviation from the median
Finally, we calculate the mean deviation (MD):
MD=Σfi|di|N=68060≈11.33
Final Answer
The median deviation from the median is approximately 11.33 Rs.
---
We have the following data:
|--------------------------|---------------------------|
| 10-20 | 4 |
| 20-30 | 6 |
| 30-40 | 10 |
| 40-50 | 20 |
| 50-60 | 10 |
| 60-70 | 6 |
| 70-80 | 4 |
The mid-point for each class interval is calculated as follows:
- For 20-30: (20 + 30)/2 = 25
- For 30-40: (30 + 40)/2 = 35
- For 40-50: (40 + 50)/2 = 45
- For 50-60: (50 + 60)/2 = 55
- For 60-70: (60 + 70)/2 = 65
- For 70-80: (70 + 80)/2 = 75
|--------------------------|---------------------------|------------------|
| 10-20 | 4 | 15 |
| 20-30 | 6 | 25 |
| 30-40 | 10 | 35 |
| 40-50 | 20 | 45 |
| 50-60 | 10 | 55 |
| 60-70 | 6 | 65 |
| 70-80 | 4 | 75 |
Now, we calculate the cumulative frequency (CF):
|--------------------------|---------------------------|---------------------------|
| 10-20 | 4 | 4 |
| 20-30 | 6 | 10 |
| 30-40 | 10 | 20 |
| 40-50 | 20 | 40 |
| 50-60 | 10 | 50 |
| 60-70 | 6 | 56 |
| 70-80 | 4 | 60 |
The total number of workers (N) is 60. To find the median class, we calculate N/2 = 60/2 = 30. The cumulative frequency just greater than 30 is 40, which corresponds to the class interval 40-50. Therefore, the median class is 40-50.
Using the median formula:
Median=l+(N/2−Ff)×h
Where:
- l = lower boundary of the median class = 40
- N = total frequency = 60
- F = cumulative frequency of the class before the median class = 20
- f = frequency of the median class = 20
- h = width of the median class = 10
Median=40+(30−2020)×10=40+(1020)×10=40+5=45
Now, we calculate the deviation di for each class:
di=Xi−Median
|------------------|-----------------|
| 15 | 15 - 45 = -30 |
| 25 | 25 - 45 = -20 |
| 35 | 35 - 45 = -10 |
| 45 | 45 - 45 = 0 |
| 55 | 55 - 45 = 10 |
| 65 | 65 - 45 = 20 |
| 75 | 75 - 45 = 30 |
Now we take the absolute values of the deviations:
|------------------|----------------------|
| 15 | 30 |
| 25 | 20 |
| 35 | 10 |
| 45 | 0 |
| 55 | 10 |
| 65 | 20 |
| 75 | 30 |
Now, we multiply the absolute deviations by their respective frequencies:
|------------------|-----------------|------|-------------------|
| 15 | 4 | 30 | 120 |
| 25 | 6 | 20 | 120 |
| 35 | 10 | 10 | 100 |
| 45 | 20 | 0 | 0 |
| 55 | 10 | 10 | 100 |
| 65 | 6 | 20 | 120 |
| 75 | 4 | 30 | 120 |
Now, we sum up the last column:
Σfi|di|=120+120+100+0+100+120+120=680
Finally, we calculate the mean deviation (MD):
MD=Σfi|di|N=68060≈11.33
The median deviation from the median is approximately 11.33 Rs.
Topper's Solved these Questions
Similar Questions
Find the mean deviation from the mean of the following data:
Classes:, 10-20, 20-30, 30-40, 40-50, 50-60, 60-70, 70-80
freequency:2, 3, 8, 14, 8, 3, 2
View SolutionCalculate the mean devation from the mean the following data:
Marks0−1010−2020−3030−4040−50No. of stu.5815166
View SolutionFind the about the mean for the following data:
Marks obtained , 10-20, 20-30, 30-40, 40-50, 50-60, 60-70, 70-80
Number of students, 2, 3, 8, 14, 8, 3, 2
View SolutionFind the mean deviation about median for the following data
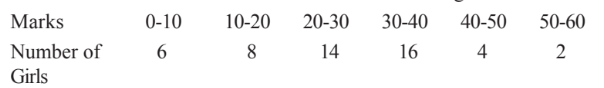
View SolutionFind the median of the following data: class : 0−10,equency:5, 10−20,3, 20−30,4, 30−40,3, 40−50,3,50-60 , 4,60-70 , 7, 70-80 , 9,80-90 , 7,90-100 , 8,
View SolutionFind the median of the following data:
Class Interval0−1010−2020−3030−4040−50f68547
View SolutionCaculate the median and mode from the following data :
Marks0−1010−2020−3030−4040−5050−6060−7070−80Number of Students 2 18 30 45 35 20 6 3
View SolutionObtain the mean , median and mode of the following data :
Marks0−1010−2020−3030−4040−5050−6060−7070−80Number of Students 5 7 15 25 20 15 8 5
View SolutionCalculate the mean and standard deviation for the following distribution: Marks:, 20-30, 30-40, 40-50, 50-60, 60-70, 70-80, 80-90 No. of students:, 3, 6, 13, 15, 14, 5, 4
View SolutionWrite the median class of the following distribution: Classes: 0-10 10-20 20-30 30-40 40-50 50-60 60-70 Frequency: 4 4 8 10 12 8 4
View Solution
