The sides of a right-angled triangle are integers. The length of one of the sides is 12. The largest possible radius of the incircle of such a triangle is-
A
2
B
3
C
4
D
5
Video Solution
Text Solution
The correct Answer is:D

Clearly
x2−y2=144
(x−y)(x+y)=144
x,y∈I
So factorsize 144 into two even factors
x+y=72 x+y=36 x+y=18
x-y=2 s-y=9 x-y=8
x=37 x=20 x-13
y=35 y=16 y=5
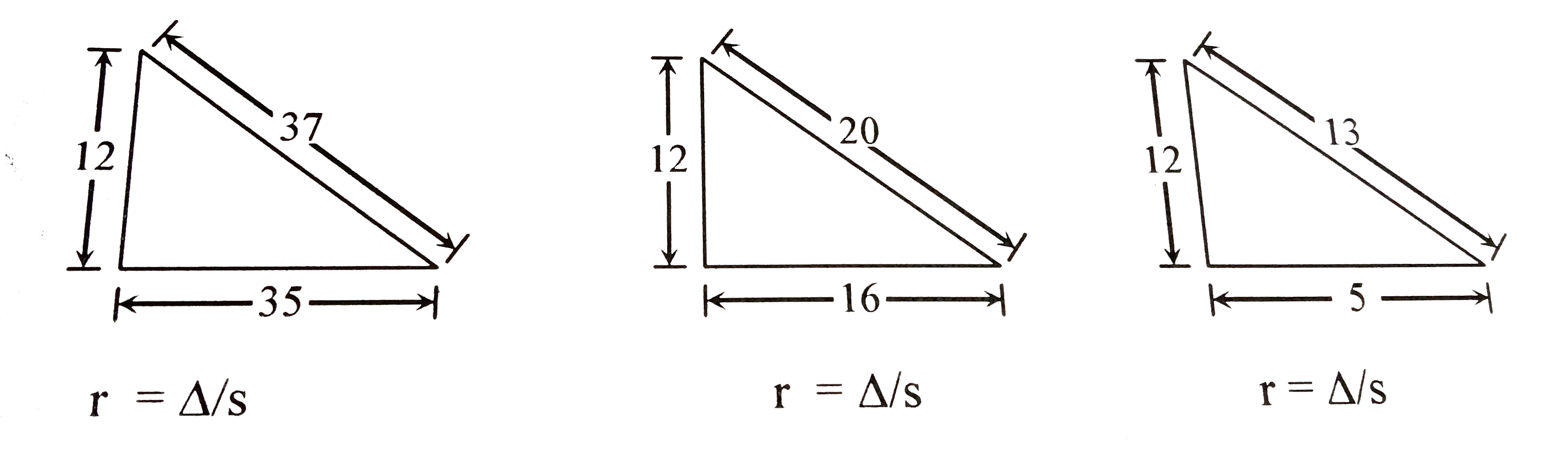
r=Δ/s r=Δ/s r=Δ/s
r=1/2×12×35(12+35+372) r=1/2×12×16(16+20+122) r=2
r=12×3584 r=12×1648
r=5 r=4
|
Similar Questions
Knowledge Check
The sides of a right-angled triangle are consecutive integers. They are
A4, 5B9, 10C12, 13D20, 21If the sides of a right angled triangle are three consecutive integers, then the length of the smallest side is
Aa) 3 unitsBb) 2 unitsCc) 4 unitsDd) 5 unitsIf the length of sides of right angled triangle are in AP, then their ratio is
A3:4:5B2:3:4C1:2:3Dnone of these
The perpendicular sides of a right angled triangle are 3x and 4x. The length of its hypotenuse is 30. Find the lengths of the perpendicular sides of the right angled triangle.
View SolutionThe length of the two sides of a right-angled triangle are equal Find the length of the hypotenuse
View SolutionTwo sides of a triangle are in the ratio 3:5 and third side is 16 .If Δ is the largest possible area of the triangle,then Δ=
View SolutionIf two sides of the right angled triangle are 3 and 4, then what is the length of the third side?
View SolutionIf A be the area of a right triangle and b one of the sides containing the right angle, prove that the length of the altitude on the hypotenuse is 2AB√b4+4A2
View Solution
