Circles C1 and C2 of radii r and R respectively, touch each other as shown in the figure. The lime l, which is parallel to the line joining the centres of C2 and C2 is tangent to C1 at P and intersects C2 at A,B.If R2=2r2, then ∠AOB equals- 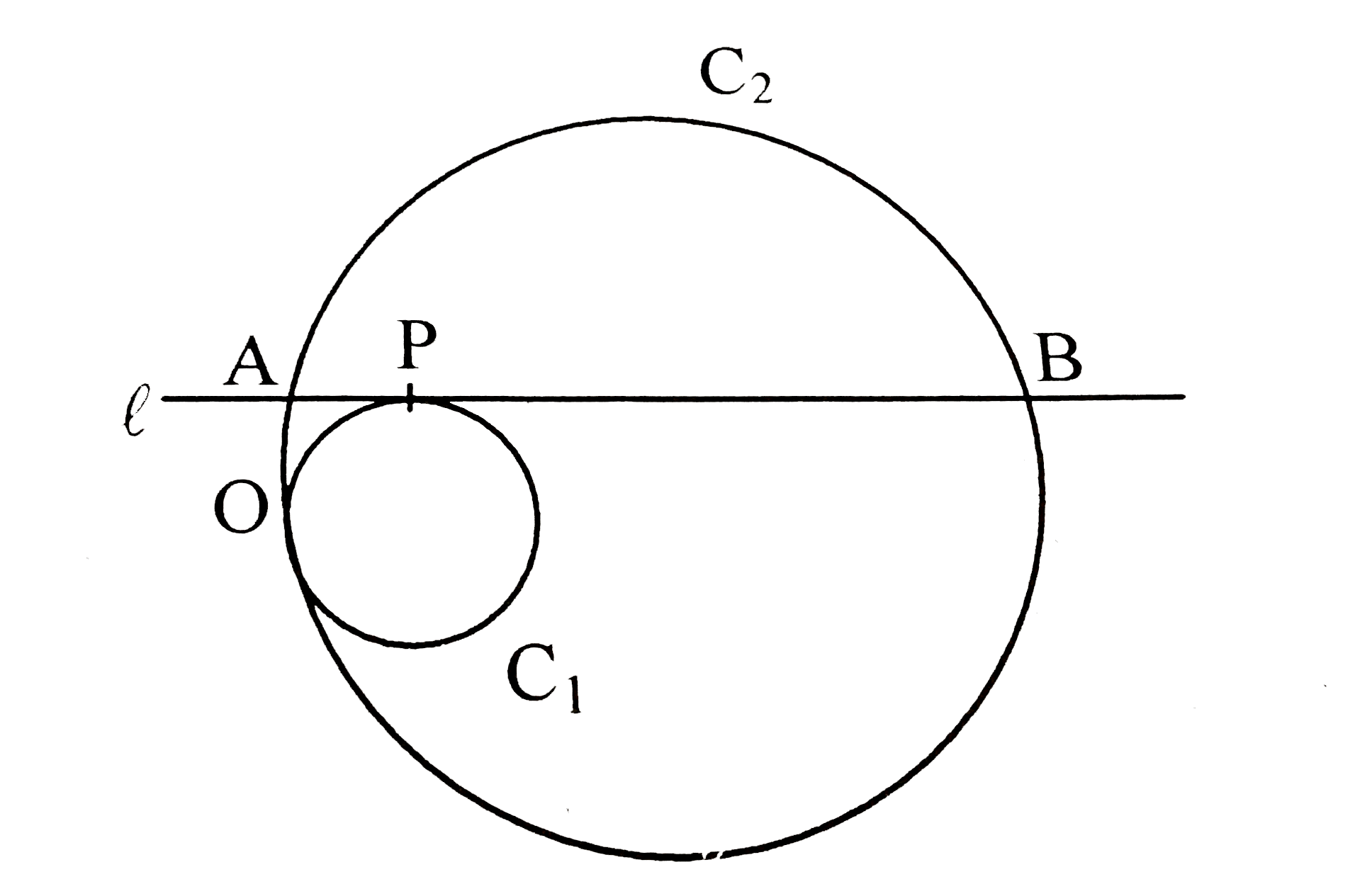
2212∘
45∘
60∘
6712∘
The correct Answer is:B

Chose AB subten 90∘ at centre.
so that AB subtend 45∘ at O (circumference of circle)
Similar Questions
Knowledge Check
There are two circles C1 and C2 of radii r1 and r2, respectively. They are mutually tangent to each other and to a line as well. There is one more circle of radius r3 which is tangent to this line and first two circles C1 and C2. What is the relation between the three radii r1,r2 and r3 ?
A1√r1+1√r2=1√r3B√r1√r2+√r2√r1=1√r3C1√r3+1√r1+1√r2Dnone of theseThe centres of two circles C1andC2 each of unit radius are at a distance of 6 unit from each other. Let P be the mid-point of the line segment joining the centres of C1andC2 and C be a circle touching circles C1andC2 externally. If a common tangent to C1 and C passing through P is also a common tangent to C2 and C, then the radius of the circle C, is
A4B8C6D3The radical axis of two circles having centres at C1 and C2 and radii r1 and r2 is neither intersecting nor touching any of the circles, if
AC1C2=0B0<C1C2<|r1−r2|CC1C2=|r1−r2|D|r1−r2|<C1C2<r1+r2
The centres of two circles C1 and C2, each of unit radius are at a distance of 6 units from each other. Let P be the mid point of the line segment joining the centres of C1 and C2, and C be a circle touching circles C1 and C2 externally. If a common tangent to C1 and C passing through P is also a common tangent to C2 and C. then the radius of the circle C is.
View SolutionTwo circles C1andC2 with equal radii r are centered at (3,2)and(6,5) respectively. If C1andC2 intersect orthogonally, then r is equal to.
View SolutionThere are two circles C1 and C2 whose radii are r1,r2, respectively. If distance between their centre is 3r1−r2 and length of direct common tangent is twice of the length of transverse common tangent. Then r1:r2 is:
View SolutionThe circle C1:x2+y2=3, with cenre at O, intersects the parabola x2=2y at the point P in the first quadrant. Let the tangent to the circle C1 at P touches other two circles C2 and C3 at R2 and R3 respectively. Suppose C2 and C3 have equal radii 2√3 and centres Q2 and Q3 respectively. If Q2 and Q3 lie on the y-axis, then Q2Q3=
View SolutionThe centres of two C1 and C2, each unit of unit radii, are at a distance of 6 units from each other. Let P be the mid-point of the line segment joining the centres of C1andC2. A third circle C is drawn such that it is externally tangent to both the circles C1andC2 at the same points where the lines passing through P are tangent to the circles C1andC2. The radius of the circle C is
View Solution
