Let ABCD be a square fo side length 1. P,Q,R,S be points in the interiors of the sides AD,BC,AB,CD, respectively , such that PQ and RS intersect at right angles .if PQ =3√34 then RS equals -
2√3
3√34
√2+12
4−2√2
The correct Answer is:B
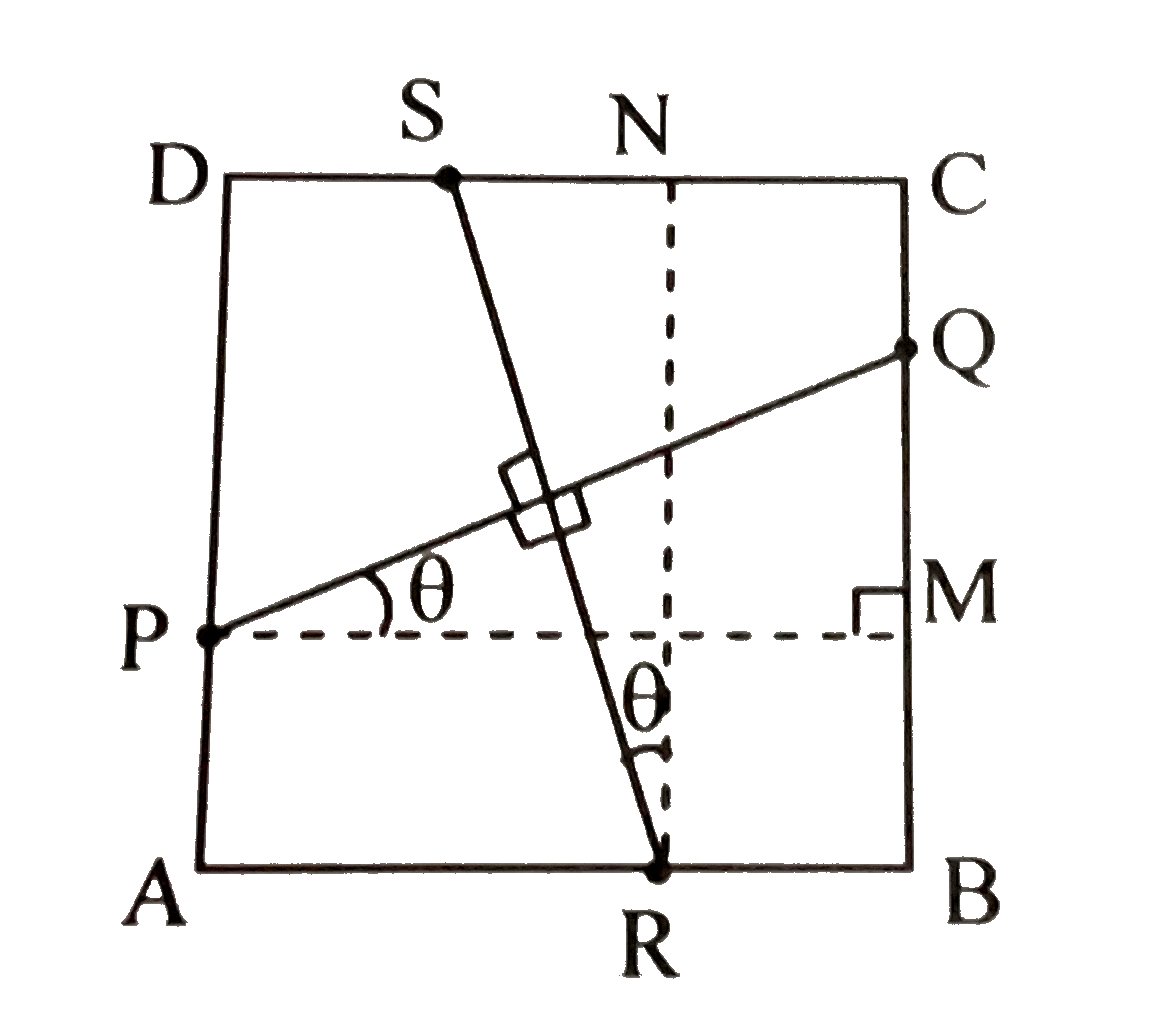
ΔPQM≅ΔRSN
SO , Rs =-PQ =3√34
Similar Questions
Let ABCD be a square of side length 1. Let P,Q,R, S bepoints in the interiors of the sides AD, BC, AB,CD,respectively, such that PQ and RS intersect at rightangles. If Po-23 then RS equalsB. 313c. 12 +1D. 4- 2125
View SolutionABCD is a square. P, Q, R, S are points on the sides AB. BC, CD, DA respectively such that AP = BQ = CR = DS. What is ∠SPQ equal to ?
View Solution
Knowledge Check
P and Q are the mid-points of the sides AB and BC, respectively, of ΔABC, right angled at B. Then:
AAQ2+CP2=AC2BAQ2+CP2=45AC2CAQ2+CP2=43AC2DAQ2+CP2=54AC2
Let ABCD be a rectangle. Let P, Q, R, S be the mid-points of sides AB, BC, CD, DA respectively. Then the quadrilateral PQRS is a
View SolutionSuppose ABCD is a rectangled and P,Q,R,S are points on the sides AB,BC,CD,DA respectively. Show that PQ+QR+RS+SP>√2AC.
View SolutionABCD is a rhombus and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionLet D(x4,y4) be a point such that ABCD is a square and M and P are the midpoints of the sides BC&CD respectively, then
View SolutionABC is a triangle and Dand E are interior points ofthe sides ABandBC respectively such that ADDB13andCEEB=3. If AEandCD intersect at F find CFFD.
View SolutionABCD is a quadrilateral; P,Q,RandS are the points of trisection of side AB,BC,CDandDA respectively and are adjacent to AandC ; prove that PQRS is parallelogram.
View Solution
