The maximum possible value of x2+y2−4x−6y,x,y∈R subject to the condition |x+y|+|x−y|=4
A
is 12
B
is 28
C
is 72
D
does not exist
Video Solution
Text Solution
The correct Answer is:B
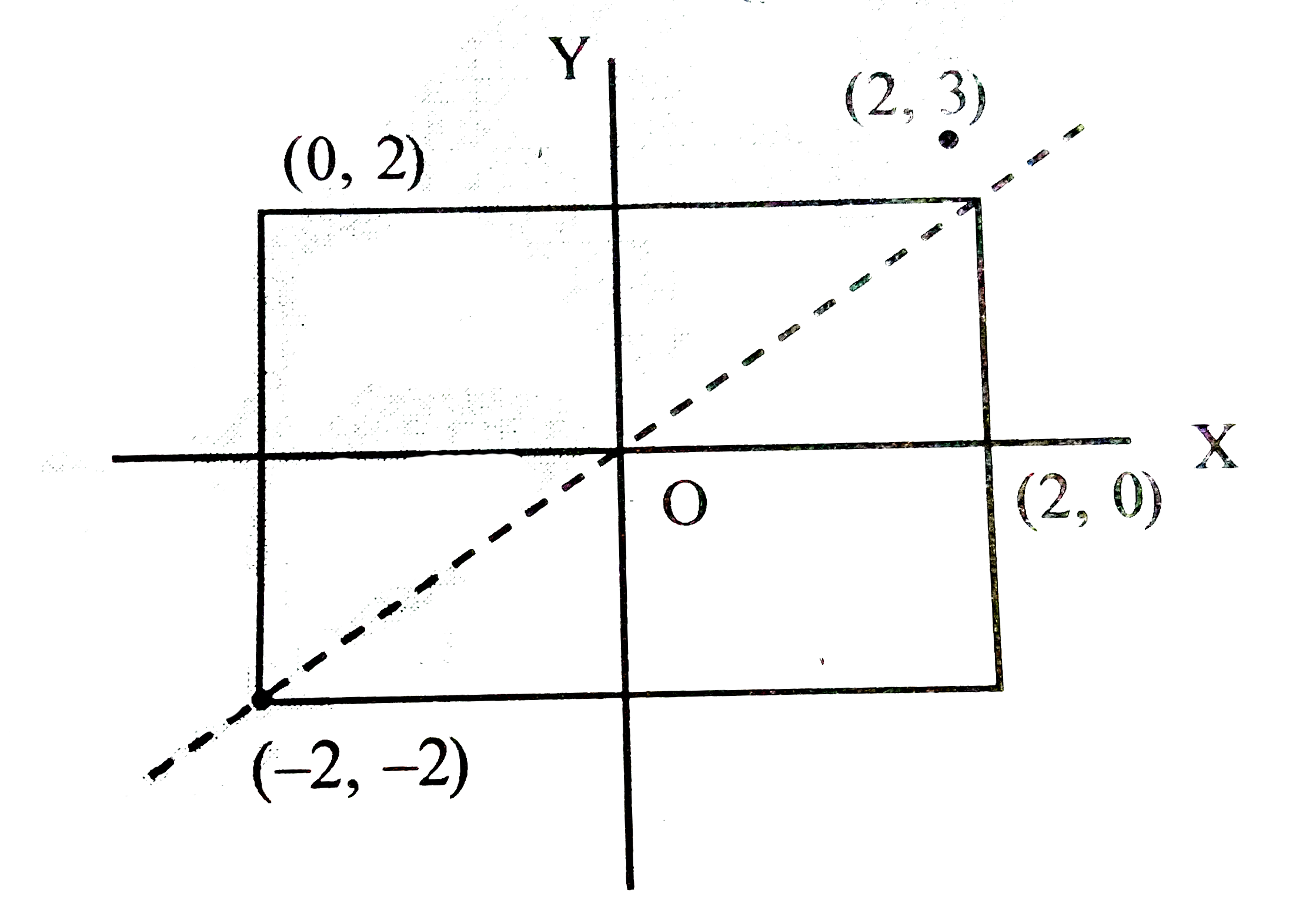
|x+y|+|x−y|=4 represent a square
x2+y2−4x−6y=(x−2)2+(y−3)2−13
=(distance point on square from (2,3))2−13
Maximum =(−2−2)2+(−2−3)2−13=28
|
Similar Questions
Knowledge Check
The maximum value of z=3x+4y subject to the conditions x+y≤40,x+2y≤10,x,y≥0 is
A130B120C40D30The minimum value of 2x + 3y subject to the condition x+4y≥8,4x+y≥12,x≥0andy≥0 is
A283B16C253D10The maximum value of Z = 4x + 2y subject to the constraints 2x+3y≤18,x+y≥10,x,y≥0 is
A20B36C40DNone of these
The maximum and minimum values of Z=5x+2y, subject to the constraints 2x+3y≥3,x−2y≥2,6x+4y≤24,−3x+2y≤3 and x,y≥0, are respectively
View SolutionThe maximum value of Z=3x+4y subject to the constraints:
x+y≤4,x≥0,y≥0 is :
View SolutionWhat is the maximum value of x⋅y subject to the condition x+y = 8 ?
View SolutionIf x2+y2−14x−6y−6=0, then the maximum possible value of 3x+4y is (where (x,y) is a point on the given curve)
View SolutionThe maximum value of z = 4x +2y subject to the constraints 2x+3y≤18,x+y≥10,x,y≥0 is
View Solution