A bulinding is in the form of a cylinder surmounted by a hemispherical valuted dome and contains $41 \frac{19}{21} m^{3}$ of air. If the internal diameter of dome is equal to its total height above the floor, find the height of the bulinding ?

Video Solution

Text Solution

Verified by Experts

Let total height bulinding = Internal dimeter of the dome = 2 r cm

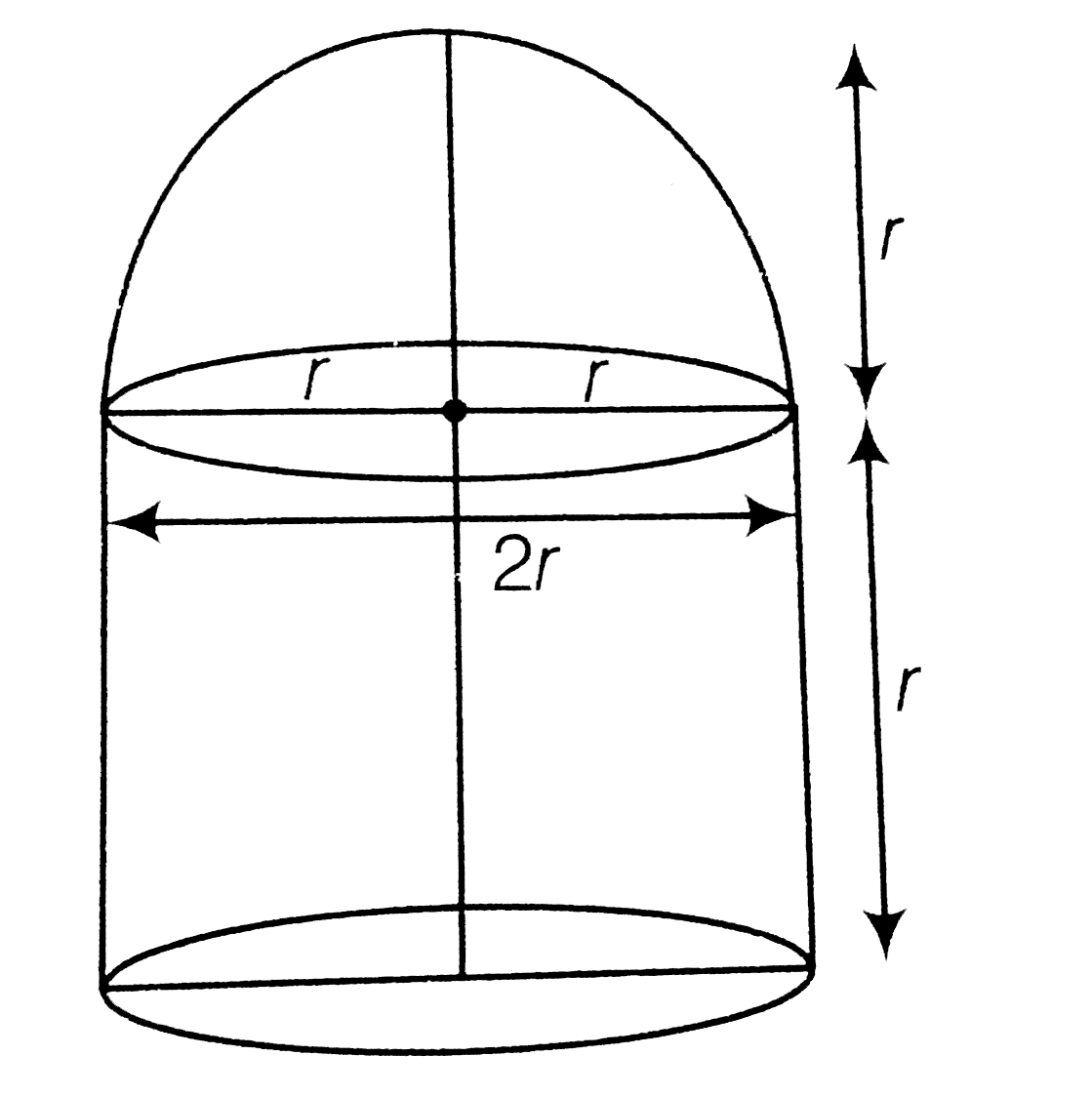
$∴$ Radius of bulinding (or dome ) $= \frac{2 r}{2} = r m$
Height of cylinder $= 2 r - r = r m$
$∴$ " " Volume of the cylinder $= π r^{2} (r) = π r^{3} m^{3}$
and volume of hemispherical dome cylinder $= \frac{2}{3} π r^{3} m^{3}$
$∴$ Total volume of the bulinding = Volume of the cylinder + Volume of hemispherical dome
$,, = (π r^{3} + \frac{2}{3} π r^{3}) m^{3} = \frac{5}{3} π r^{3} m^{3}$
According to the question,
volume of the buliding = Volume of the air
$\Rightarrow \frac{5}{3} π r^{3} = 41 \frac{19}{21}$
$\Rightarrow,, \frac{5}{3} π r^{3} = \frac{880}{21}$
$\Rightarrow r^{3} = \frac{880 \times 7 \times 3}{21 \times 22 \times 5} = \frac{40 \times 21}{21 \times 5} = 8$
$\Rightarrow r^{3} = 8 \Rightarrow r = 2$
$∴$ " " Height of the buliding $= 2 r = 2 \times 2 = 4 m$

Updated on:21/07/2023