In Figure, ABCD is a rectangle. BM and DN are perpendicular from B and D respectively on AC . Prove that MBC≅DNA (ii) BM=DN
The correct Answer is:Yes
Step by step video, text & image solution for In Figure, A B C D is a rectangle. B M\ a n d\ D N are perpendicular from B\ a n d\ D respectively on A C . Prove that M B C~= D N A (ii) B M=D N by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PARALLELOGRAMSBOOK - RS AGGARWALCHAPTER - PARALLELOGRAMSEXERCISE - Exercise 16B
10 Videos
- PARALLELOGRAMSBOOK - RS AGGARWALCHAPTER - PARALLELOGRAMSEXERCISE - Exercise 16B
10 Videos
- OPERATIONS ON ALGEBRAIC EXPRESSIONSBOOK - RS AGGARWALCHAPTER - OPERATIONS ON ALGEBRAIC EXPRESSIONSEXERCISE - Exercise 6E (Tick the correct answer in each of the following:)
19 Videos
- PERCENTAGEBOOK - RS AGGARWALCHAPTER - PERCENTAGEEXERCISE - TEST PAPER -9 ( TRUE AND FALSE )
4 Videos
Similar Questions
ABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM . Prove that LM and BD bisect each other.
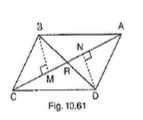
View SolutionIn Figure, BM and DN are both perpendiculars to the segments AC and BM=DN . Prove that AC bisects BD
View SolutionBD is one of the diagonals of a quadrilateral ABCD. AM and CN are the perpendiculars from A and C , respectively, on BD. Show That ar (qua..ABCD)=12BD.AM+CN
View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE trisect (divide into three equal parts) the diagonal BD .
View SolutionIn a ABC, BM and CN are perpendiculars from B and C respectively on any line passing through A. If L is the mid-point of BC , prove that ML=NL .
View SolutionIn Figure, ABCD is a rectangle with sides AB=10cmandAD=5cm Find the area of EFG

View SolutionIn a ABC, If LandM are points on ABandAC respectively such that LMparallelBC
Prove that: ar(LCM)=ar(LBM)
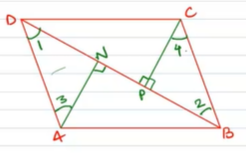
View SolutionIn Figure, AN and CP are perpendicular to the diagonal BD of a parallelogram ABCD. Prove that : ADN≅CBP (ii) AN=CP
View SolutionIn a ABC, If LandM are points on ABandAC respectively such that LMparallelBC
Prove that: ar(LBC)=ar(MBC)
View SolutionIn Figure, find the four angles A, B, C and D in the parallelogram ABCD

View Solution
