Each side of a square park is 80 m. At each corner of the park there is a flower bed in the form of a quadrant of a circle of radius 14 m, as shown in the figure. Find the area of the remaining part of the park.
The correct Answer is:5784m2
To solve the problem step by step, we will calculate the area of the square park and then subtract the area of the flower beds (quadrants of circles) from it.
Step 1: Calculate the area of the square park
The formula for the area of a square is:
Area=side2
Given that each side of the square park is 80 m:
Area=80×80=6400m2
Step 2: Calculate the area of one quadrant of a circle
The formula for the area of a full circle is:
Area=πr2
Since we have a quadrant (which is one-fourth of a circle), the area of one quadrant is:
Area of one quadrant=14πr2
Given that the radius r is 14 m:
Area of one quadrant=14×227×(14)2
Calculating (14)2:
(14)2=196
Now substituting this into the equation:
Area of one quadrant=14×227×196
Calculating further:
=22×1964×7
=22×19628
Now simplifying 19628=7:
=22×7=154m2
Step 3: Calculate the area of four quadrants
Since there are four corners, we multiply the area of one quadrant by 4:
Area of four quadrants=4×154=616m2
Step 4: Calculate the area of the remaining part of the park
To find the area of the remaining part of the park, we subtract the area of the flower beds from the area of the square park:
Area of remaining part=Area of square−Area of four quadrants
=6400−616=5784m2
Final Answer
The area of the remaining part of the park is:
5784m2
The formula for the area of a square is:
Area=side2
Given that each side of the square park is 80 m:
Area=80×80=6400m2
The formula for the area of a full circle is:
Area=πr2
Since we have a quadrant (which is one-fourth of a circle), the area of one quadrant is:
Area of one quadrant=14πr2
Given that the radius r is 14 m:
Area of one quadrant=14×227×(14)2
Calculating (14)2:
(14)2=196
Now substituting this into the equation:
Area of one quadrant=14×227×196
Calculating further:
=22×1964×7
=22×19628
Now simplifying 19628=7:
=22×7=154m2
Since there are four corners, we multiply the area of one quadrant by 4:
Area of four quadrants=4×154=616m2
To find the area of the remaining part of the park, we subtract the area of the flower beds from the area of the square park:
Area of remaining part=Area of square−Area of four quadrants
=6400−616=5784m2
The area of the remaining part of the park is:
5784m2
Topper's Solved these Questions
- MENSURATIONBOOK - RS AGGARWALCHAPTER - MENSURATIONEXERCISE - EXERCISE 20A
20 Videos
- MENSURATIONBOOK - RS AGGARWALCHAPTER - MENSURATIONEXERCISE - EXERCISE 20B
16 Videos
- LINES AND ANGLESBOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Exercise 13
11 Videos
- PERCENTAGE BOOK - RS AGGARWALCHAPTER - PERCENTAGE EXERCISE - TEST PAPER
16 Videos
Similar Questions
A square park has each side of 100 m. At each corner of the park, there is a flower bed in the form of a quadrant of radius 14 m as shown in Fig. 15.37. Find the area of the remaining part of the park (Use π=22/7) . (FIGURE)
View SolutionIn each of the corners, there is a flower bed in the form of a quadrant of a circle of radius 2 m. Also, there is a flower bed in the form of a circle of radius 2 m in the middle of the plot. Find the area of the remaining plot.

View Solution
Knowledge Check
A square park has each side 50 m. At each corner of the park, there is a flower bed in the form of a quadrant of radius 7 m, as shown in the figure. Find the area of remaining part of the park.
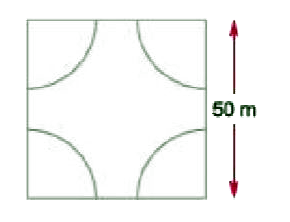 A2346 sq mB2340 sq mC2250 sq mD2155 sq m
A2346 sq mB2340 sq mC2250 sq mD2155 sq mThe side of a square park is 100 m. Perimeter of the park is:
A1000 mB400 mC200 mD800 mFive square flower beds each of sides 1.2 m are dug on a piece of land 4.8 m long and 4.2 m wide. What is the area of the remaining part of the land ?
A12.69 sq. mB12.96 sq. mC11.96 sq. mD144 sq. m
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in Fig. 12.23. Find the area of the remaining portion of the square.
View SolutionFive square flower beds each of sides 1 m are dug on a piece of land 5 m long and 4 m wide. What is the area of the remaining part of the land?
View SolutionFrom a square of side 8 cm, two quadrants of a circle of radii 1.4 cm are cut from two corners. Another circle of radius 4.2 cm is also cut from the centre as shown in the figure. Find the area of the remaining (shaded) portion of the square. [Take π=227]

View SolutionFrom a square of side 8 cm, two quadrants of a circle of radii 1.4 cm are cut from two corners . Another circle of radius 4.2 cm is also cut from the centre as shown in the figure . Find the area of the remaining (shaded) portion of the square . [Takeπ=227]
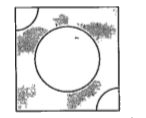
View SolutionA park is in the form of a circle with radius 35m. At the centre of the park, there is a lawn in the form of a square. If the area of the park, excluding the lawn is 2500m2 find the cost of levelling the lawn at the rate of Rs 50 per m2
View Solution
