In a △ABC, if ∠A=90∘, then BC2 = (.....) + (.....).
The correct Answer is:AB2,AC2
To solve the problem, we need to apply the Pythagorean theorem to triangle ABC, where angle A is 90 degrees. Here's the step-by-step solution:
Step 1: Identify the triangle and its sides
In triangle ABC, we know:
- Angle A = 90 degrees (right angle)
- Side AB is perpendicular to side AC
- Side BC is the hypotenuse of the triangle
Step 2: Apply the Pythagorean theorem
According to the Pythagorean theorem, in a right triangle, the square of the length of the hypotenuse (BC) is equal to the sum of the squares of the lengths of the other two sides (AB and AC). Mathematically, this is expressed as:
BC2=AB2+AC2
Step 3: Write the final expression
From the application of the Pythagorean theorem, we can conclude:
BC2=AB2+AC2
Step 4: Fill in the blanks
Thus, we can fill in the blanks in the given statement:
BC2=AB2+AC2
Final Answer:
BC² = AB² + AC²
---
In triangle ABC, we know:
- Angle A = 90 degrees (right angle)
- Side AB is perpendicular to side AC
- Side BC is the hypotenuse of the triangle
According to the Pythagorean theorem, in a right triangle, the square of the length of the hypotenuse (BC) is equal to the sum of the squares of the lengths of the other two sides (AB and AC). Mathematically, this is expressed as:
BC2=AB2+AC2
From the application of the Pythagorean theorem, we can conclude:
BC2=AB2+AC2
Thus, we can fill in the blanks in the given statement:
BC2=AB2+AC2
BC² = AB² + AC²
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - TEST PAPER (True/False)4videos
CONSTRUCTIONS
- BOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - TEST PAPER (M.C.Q)7videos
CONSTRUCTIONS
- BOOK - RS AGGARWALCHAPTER - CONGRUENCEEXERCISE - EXERCISE18videos
CONGRUENCE
- BOOK - RS AGGARWALCHAPTER - DECIMALSEXERCISE - TEST PAPER-3(D)5videos
DECIMALS
Similar Questions
Knowledge Check
- Question 1 - Select One
In a △ABC, if ∠B=40∘ and ∠C=35∘, then ∠A=?
A50∘B55∘C105∘D150∘ - Question 2 - Select One
In a △ABC,if 2∠A=3∠B=6∠C, then ∠B=?
A30∘B45∘C60∘D90∘ - Question 3 - Select One
In △ABC, ∠B=90∘ , AB=5cm and AC=13cm. Then, BC = ?
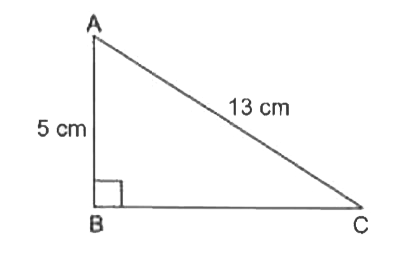 A8 cmB18 cmC12 cmDnone of these
A8 cmB18 cmC12 cmDnone of these

