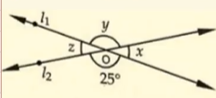
In the given figure, x:y = 2:3 and ∠ACD=120∘. Find the values of x y and z.
The correct Answer is:x=48,y=72,z=60
To solve the problem, we need to find the values of angles x, y, and z given that the ratio x:y = 2:3 and angle ACD = 120 degrees.
1. Understanding the Ratio:
Given the ratio x:y = 2:3, we can express y in terms of x.
Let x = 2k and y = 3k for some constant k.
2. Using the Exterior Angle Theorem:
According to the Exterior Angle Theorem, the exterior angle (angle ACD) is equal to the sum of the two opposite interior angles (x and y).
Therefore, we can write the equation:
x+y=120∘
3. Substituting the Values:
Substitute the expressions for x and y into the equation:
2k+3k=120∘
This simplifies to:
5k=120∘
4. Solving for k:
Divide both sides by 5 to find k:
k=120∘5=24∘
5. Finding x and y:
Now substitute k back into the expressions for x and y:
x=2k=2×24∘=48∘
y=3k=3×24∘=72∘
6. Finding z:
In a triangle, the sum of the angles is always 180 degrees. Therefore, we can find z as follows:
z=180∘−(x+y)=180∘−(48∘+72∘)=180∘−120∘=60∘
Final Values:
- x=48∘
- y=72∘
- z=60∘
Given the ratio x:y = 2:3, we can express y in terms of x.
Let x = 2k and y = 3k for some constant k.
According to the Exterior Angle Theorem, the exterior angle (angle ACD) is equal to the sum of the two opposite interior angles (x and y).
Therefore, we can write the equation:
x+y=120∘
Substitute the expressions for x and y into the equation:
2k+3k=120∘
This simplifies to:
5k=120∘
Divide both sides by 5 to find k:
k=120∘5=24∘
Now substitute k back into the expressions for x and y:
x=2k=2×24∘=48∘
y=3k=3×24∘=72∘
In a triangle, the sum of the angles is always 180 degrees. Therefore, we can find z as follows:
z=180∘−(x+y)=180∘−(48∘+72∘)=180∘−120∘=60∘
- x=48∘
- y=72∘
- z=60∘
Topper's Solved these Questions
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - TEST PAPER (M.C.Q)
7 Videos
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - TEST PAPER (Fill in the blanks)
5 Videos
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE C(M.C.Q)
38 Videos
- CONGRUENCEBOOK - RS AGGARWALCHAPTER - CONGRUENCEEXERCISE - EXERCISE
18 Videos
- DECIMALSBOOK - RS AGGARWALCHAPTER - DECIMALSEXERCISE - TEST PAPER-3(D)
5 Videos
Similar Questions
Knowledge Check
In the given figure find the values of x and y.
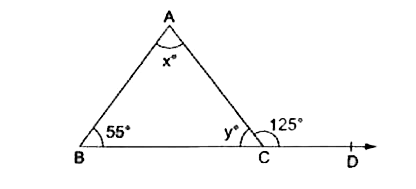 Ax=70 and y=65Bx=70 and y=55Cx=55 and y=70Dx=80 and y=55
Ax=70 and y=65Bx=70 and y=55Cx=55 and y=70Dx=80 and y=55
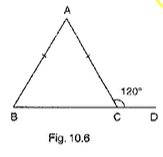
In Figure, AB=AC and ∠ACD=1200. Find ∠A
View SolutionIn the given figure, AB||CD. Find the values of x,y and z.

View SolutionIn the given figure, AB∣∣CD. Find th value of x,y and z.

View SolutionIf x=1,y=2and z=5, find the value of 3x–2y+z.
View SolutionIn the given figure, find the value of x and y.
View SolutionIn the given figure, AB||CD||EF, ∠DBG=x, ∠EDH=y, ∠AEB=z, ∠EAB=90∘ and ∠BEF=65∘. Find the values of x, y, and z.
View SolutionIf x:y=2:3, y:z=3:4, z:k=1:2, find the value of x:y:z:k
View Solution