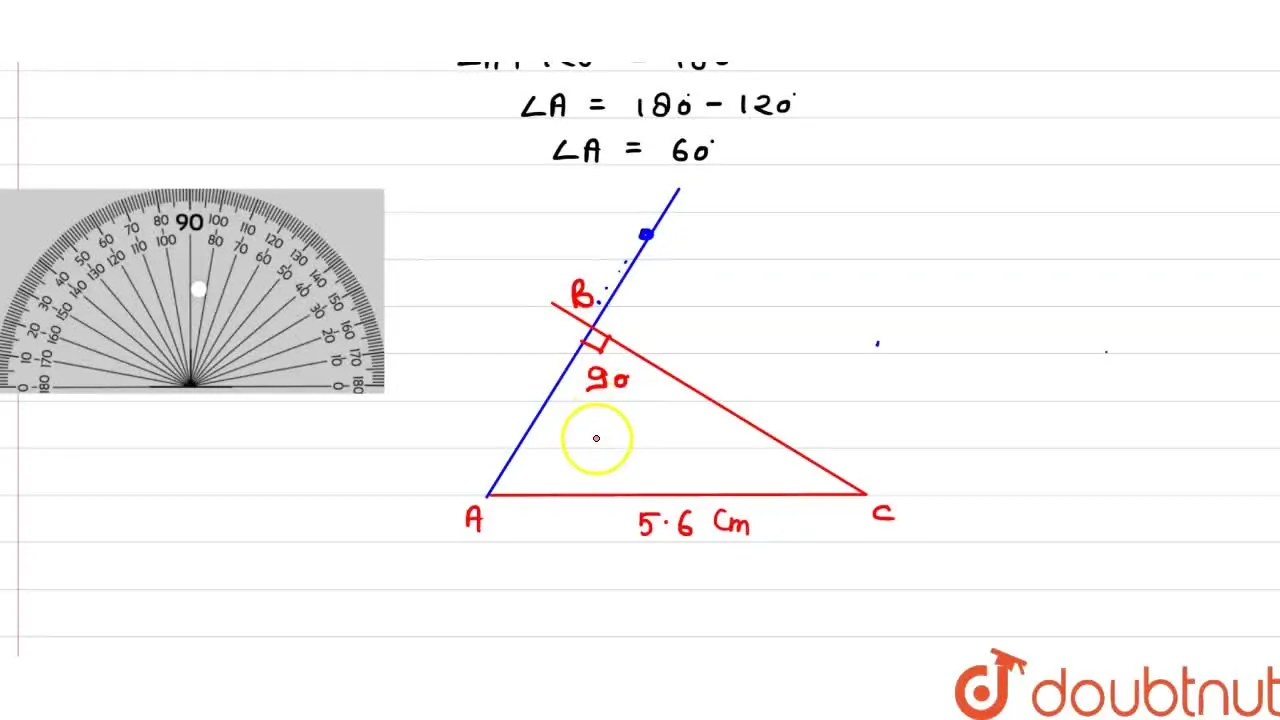
Construct a right-angled triangle whose hypotenuse measures 5.6 cm and one of whose acute angles measures 30∘.
The correct Answer is:∠C=180∘−120∘=60∘
Step by step video, text & image solution for Construct a right-angled triangle whose hypotenuse measures 5.6 cm and one of whose acute angles measures 30^(@). by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE A3videos
CONSTRUCTIONS
- BOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE B10videos
CONSTRUCTIONS
- BOOK - RS AGGARWALCHAPTER - CONGRUENCEEXERCISE - EXERCISE18videos
CONGRUENCE
- BOOK - RS AGGARWALCHAPTER - DECIMALSEXERCISE - TEST PAPER-3(D)5videos
DECIMALS
Similar Questions
Draw a right triangle having hypotenuse of length 5.4 cm, and one of the acute angles of measure300.
View SolutionDraw a right triangle having hypotenuse of length 5.4 cm, and one of the acute angles of measure 600.
View SolutionConstruct a right angled triangle with hypotenuse √13cm. Draw a circumcircle of this triangle.
View SolutionThe sides of a right triangle whose hypotenuse is 17cm are and
View SolutionIn a right-angled triangle, If one angle ahs measures 75∘, then the another angle has measure.
View SolutionConstruct a right angled triangle whose base is 12cm and sum of its hypotenuse and other side is 18cm.
View SolutionThe base of a right-angled triangle measures 48 cm and its hypotenuse measures 50 cm. Find the area of the triangle.
View SolutionThe base of a right - angled triangle measures 48 cm and its hypotenuse measures 50 cm . Find the area of the triangle .
View SolutionFind the area of a right triangle whose hypotenuse is 17 cm and one of the sides which forms a right angle is 8 cm .
View SolutionDraw a right triangle whose hypotenuse is of length 4 cm and one side is of length 2.5 cm.
View Solution