AM is median of △ABC, prove that (AB+BC+CA)>2AM.
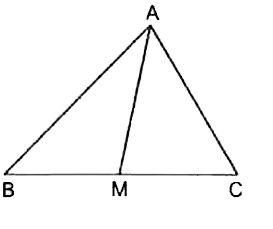
Step by step video & image solution for AM is median of triangleABC, prove that (AB+BC+CA)gt2AM. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - EXERCISE 15-D18videos
PROPERTIES OF TRIANGLES
- BOOK - RS AGGARWALCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - EXERCISE 15-B8videos
PROPERTIES OF TRIANGLES
- BOOK - RS AGGARWALCHAPTER - PROPERTIES OF PARALLEL LINE EXERCISE - EXERCISE 1415videos
PROPERTIES OF PARALLEL LINE
- BOOK - RS AGGARWALCHAPTER - RATION AND PROPORTION EXERCISE - Test papers18videos
RATION AND PROPORTION
Similar Questions
In the given figure ,P is a point on the side BC of △ABC.Prove tat (AB+BC+AC)GT2AP
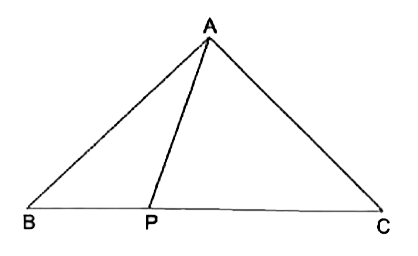 View Solution
View SolutionAM is a median of s triangle ABC. Is AB+BC+CA>2AM? (Consider the sides of triangles ΔABMandΔAMC.
View SolutionIn ΔABC,D is any point on side BC. Prove that
AB+BC+CA>2ADView SolutionIn the figure, AD is perpendicular to BC, prove that AB+AC>2AD.
 View Solution
View SolutionIf O is point in the exterior of △ABC,show that 2(OA+OB+OC)>(AB+BC+CA)
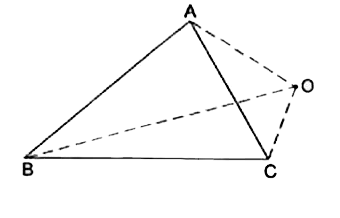 View Solution
View SolutionAD is a median of the ΔABC.Is it trure AB+BC+CA>2AD? Give reason for your answer
View SolutionAD,BE and CF are the medians of a ΔABC. Prove that 2(AD+BE+CF)<3(AB+BC+CA)<4(AD+BE+CF)
View SolutionSeg AD is the median of △ABC and AM⊥BC. Prove that : (i)AC2=AD2+BC×DM+(BC2)2 (ii)AB2=AD2−BC×DM+(BC2)2.
View SolutionIn △ ABC, AD is a median. Prove that AB + AC > 2AD
View SolutionIn △ABC, in the usual notation, the area is 12 bc sq. units AD is the median to BC. Prove that ∠ABC=12∠ADC.
View Solution
