If AB=QR, BC=PR and CA=PQ then
ΔABC≅ΔPQR
ΔCBA≅ΔPRQ
ΔBAC≅ΔRPQ
ΔPQR≅ΔBCA
The correct Answer is:B
We know that,if ΔRST is congruent to ΔUVW i.e, ΔRST≅ΔUVW, then sides of ΔRST fall on corresponding equal sides of ΔUVW and angels of ΔRST fall on corresponding equal angles of ΔUVW.
Here given AB=QR,BC=PR and CA=PQ,which shows that AB covers QR,BC covers PR and CA covers PQ,i.e, A correspond to Q,B correspond to R and C correcpond P
of A↔Q,B↔R,C↔P
Under this correspondence,
ΔABC≅ΔQRP ,so option (a) is incorrect.
or ΔBAC≅ΔRQP ,so option ( c) is incorrect.
ΔCBA≅ΔPRQ ,so option (b ) is correct.
ΔBCA≅ΔRPQ ,so option (d) is incorrect.
Topper's Solved these Questions
Similar Questions
Given: In △ABC and △PQR, AB=PQ, BC=QR and CB and RQ are extended to X and Y respectively and ∠ABX=∠PQY. Prove that ABC≅ PQR
View SolutionTriangles ABC and PQR are both isosceles with AB=AC and PO=PR respectively. If also, AB=PQ and BC=QR, are the two triangles congruent? Which condition do you use? If△B= 500, what is the measure of∠R?
View Solution
Knowledge Check
In ΔDEFandΔPQR, if PQ =DE, EF=PR and FD =QR, then
AΔDEF≅ΔRPQBΔDEF≅ΔQPRCΔDEF≅ΔQRPDΔDEF≅ΔPQRIn ΔDEFandΔPQR, if PQ = DE , EF = PR and FD = QR , then
AΔDEF≅ΔRPQBΔDEF≅ΔQRPCΔDEF≅ΔPQRDΔDEF≅ΔQPRIn ΔDEFandΔPQR, if PQ =DE, EF=PR and FD =QR, then
AΔDEF≡ΔRPQBΔDEF≡ΔQPRCΔDEF≡ΔQRPDΔDEF≡ΔPQR
Which of the following pairs of triangles are congruent ? Also state the condition of congruency in each case :

(iv) In ΔABC and ΔDEF,AB=EF,BC=DF and ∠B=∠F
(v) In ΔABC and ΔPQR,AB=QR,AC=PR and ∠B=∠R
(vi) In ΔABC and ΔPQR,∠A=∠P,AC=PR and AB=PQ
(vi) In ΔABC and ΔPQR,AB=QR,∠A=∠Q and AC=QP.
View SolutionIn ΔABC and ΔPQR , in a one-to-one correspondance ABQR=BCPR=CAPQ then……
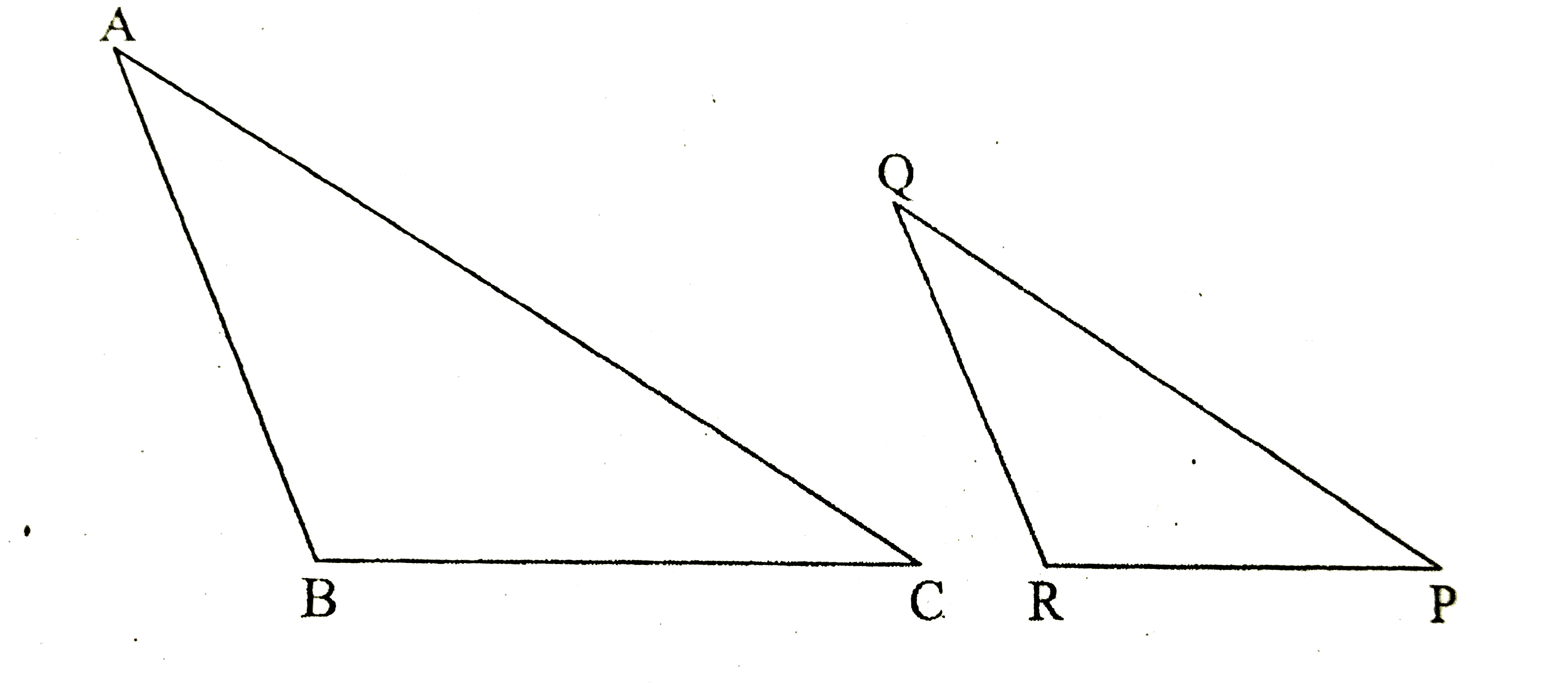
View SolutionIn ΔABCandΔPQR, in a one to one correspondence.
ABQR=BCPR=CAPQ, then
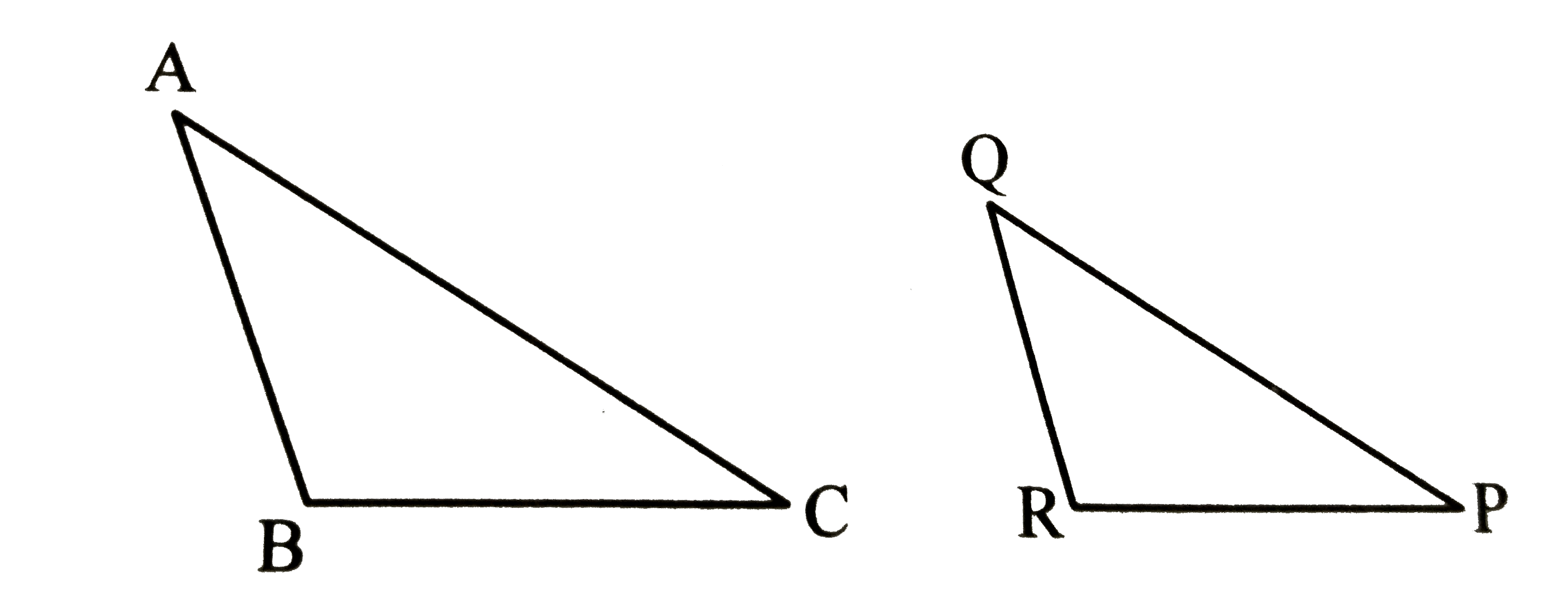
View SolutionIi ΔPQR, PD⊥QR such that D lies on QR, if PQ=a,PR=b,QD=c and DR=d, then prove that (a+b)(a-b)=(c+d)(c-d).
View SolutionΔPQRandΔTQR are on the same base QR and on the same side of QR . If PQ = TR and PR = TQ, then which of the following is correct ?
View Solution