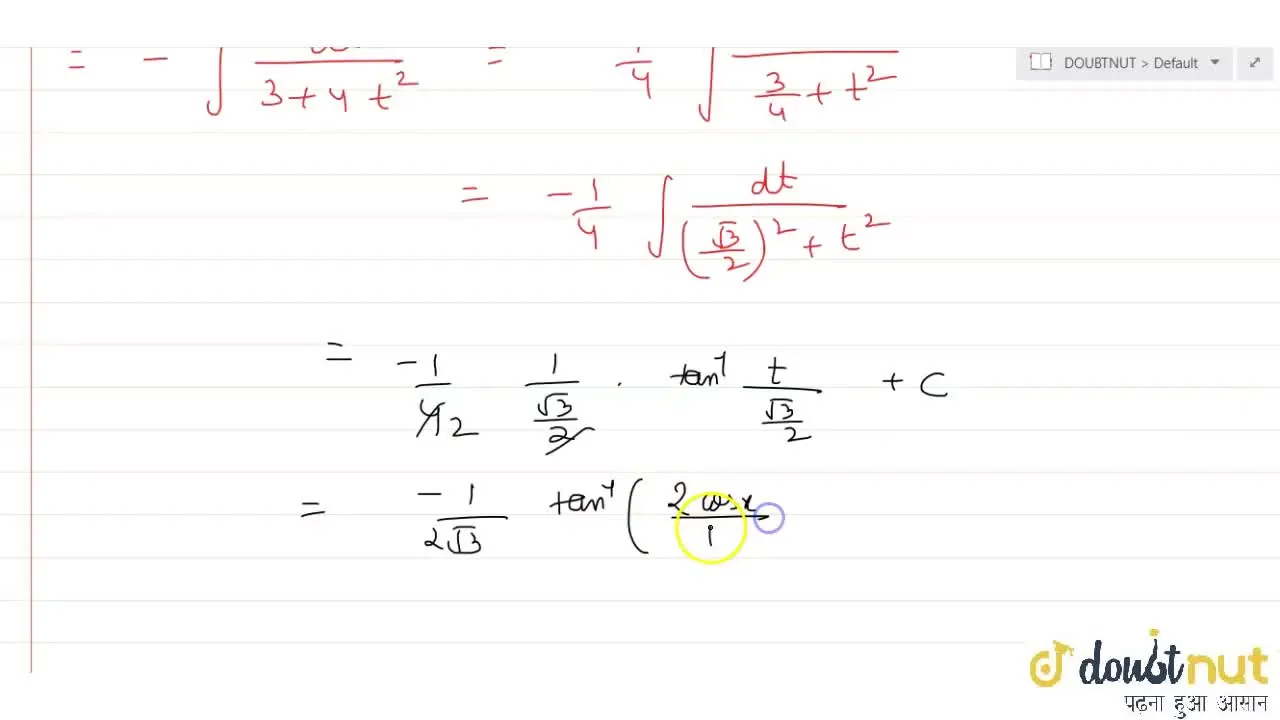∫sinx3+4cos2xdx
Video Solution
Text Solution
The correct Answer is:N/a
Let I=∫sinx3+4cos2xdx
Put cosx=t⇒−sinxdx=dt
I=−∫dt3+4t2=−14∫dt(√322)+t2
=−14.2√3tan−1'2t√3+C
=−12√3tan−1'(2cosx√3)+C
|
Updated on:21/07/2023
Related Playlists
Similar Questions
∫sinxcos2xdx=
View SolutionEvaluate : (i) ∫sinx(1−4cos2x)dx
(ii) ∫cosec2x(1−cot2x)dxView Solution∫sinx(1+cos2x)dx
View SolutionEvaluate : (i) ∫cos3xsinxdx (ii) ∫(√sinx)cosxdx (iii) ∫cosec2x(1+cotx)dx (iv) ∫sinx(3+4cosx)2dx
View Solution∫sinx√4−cos2xdx=
View Solution∫sinx1+cos2xdx
View Solution(i)∫sinxcos5xdx
View Solution1.∫sinxcos7xdx
View Solution∫sinx(3+4cosx)3dx
View Solution∫sinx(3+4cosx)3dx
View Solution