is a
A
a contradiction
B
a tautology
C
either tautology or contradiction
D
neither tautology nor contradiction
Video Solution
Text Solution
The correct Answer is:A
|
Answer
Step by step video, text & image solution for (p ^^ ~q) ^^ (~p ^^ q) is a by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MATHEMATICAL REASONING BOOK - FIITJEECHAPTER - MATHEMATICAL REASONING EXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE)
16 Videos
- MATHEMATICAL REASONING BOOK - FIITJEECHAPTER - MATHEMATICAL REASONING EXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-1
24 Videos
- MATHEMATICAL REASONING BOOK - FIITJEECHAPTER - MATHEMATICAL REASONING EXERCISE - CHAPTER PRACTICE PROBLEMS (SUBJECTIVE)
5 Videos
- INDEFINTE INTEGRALBOOK - FIITJEECHAPTER - INDEFINTE INTEGRALEXERCISE - EXERCISE-8
1 Videos
- MATHEMATICS BOOK - FIITJEECHAPTER - MATHEMATICS EXERCISE - NUMERICAL DECIMAL BASED QUESTIONS
15 Videos
Similar Questions
Knowledge Check
(p∧~q)∧(~p∨q) is
Aa contradictionBa tautologyCEither (a) or (b)DNeigher (a) nor (b)The proposition (p∧q)∧(p→~q) is
AContradictionBTautologyCContingencyDTautology and ContradictionQuivalent circuit for the logical expression (~p∧q)∨(~p∧~q)∨(p∧~q) is
A B
B C
C D
D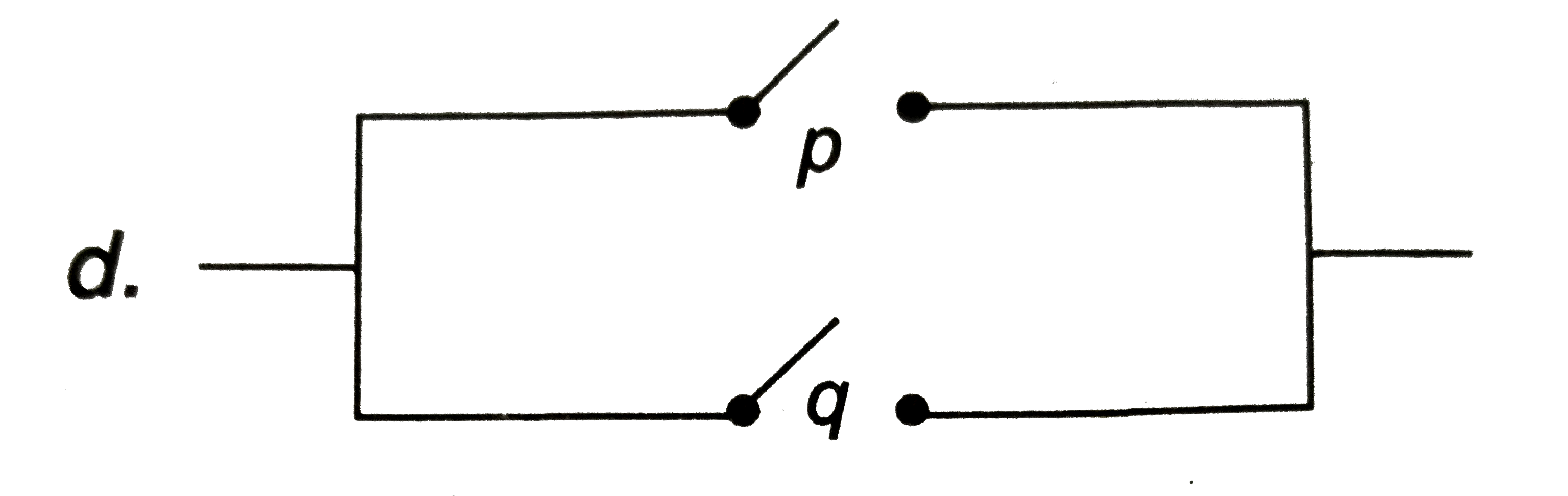
If p and q and q are two statements , prove that (i) ~(p∨q)≡(~p)∧(q) " " (ii) ~( p ^^ q) = (~p) v(~q)
View SolutionThe boolean expression ((p∧q)∨(p∨~q))∧(~p∨q) is equivalent to
View SolutionThe negation of (~p∧q)∨(p∧~q) is
View Solutionp∧(q∧r)=(p∧q)∧r is
View SolutionThe property ~(p∧q)≡~p∨~q is called
View Solution
