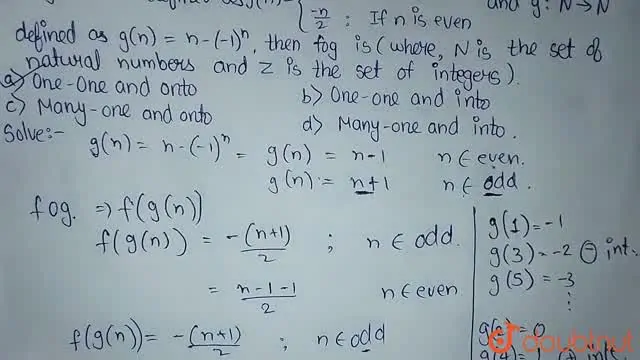If f:N→Z defined as f(n)=⎧⎨⎩n−12: if n is odd−n2: if n is even and g:N→N defined as g(n)=n−(−1)n, then fog is (where, N is the set of natural numbers and Z is the set of integers)
one - one and onto
one - one and into
many - one and onto
many - one and into
The correct Answer is:A
Step by step video, text & image solution for If f:NrarrZ defined as f(n)={{:((n-1)/(2),":"," if n is odd"),((-n)/(2),":", " if n is even"):} and g:NrarrN defined as g(n)=n-(-1)^(n), then fog is (where, N is the set of natural numbers and Z is the set of integers) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
If f:N→N is defined by f(n)=n−(−1)n, then
View SolutionThe mapping f : N→Ngiven by f(n)=1+n2,n∈N where, N is the set of natural numbers is
View SolutionThe mapping f : N→N given by f(n)=1+n2,n∈N, where N is the set of natural numbers, is
View SolutionThe function f:N→N defined by f(x)=x−5[x5] where N is a set of natural numbers, then
View SolutionThe function f:N→N,N being the set of of natural numbers, defined by f(x)=2x+3 is
View SolutionThe mapping f : N→N given by f(n)=1+n2,n∈N, where N is the set of natural numbers, is
View SolutionShow that f:n→N defined by f(n)={((n+12,(ifnisodd)),(n2,(ifniseven)) is many -one onto function
View SolutionThe function f:N→N (N is the set of natural numbers defined by f(n)=2n+3 is :
View SolutionThe function f:N→N (N is the set of natural numbers defined by f(n)=2n+3 is :
View SolutionLet f: W→W be defined by: f(n)={n−1,if n is oddn+1,if n is even. Show that 'f' is invertible. Find the inverse of 'f'. (Here 'W' is the set of whole numbers.)
View Solution