Two point masses, m each carrying charges and are attached to the ends of a massless rigid non - conducting wire of length L. When this arrangement is placed in a uniform electric field, then it deflects through an angle . The minimum time needed by the rod to align itself along the field is
The correct Answer is:B
To solve the problem, we need to analyze the forces acting on the two point masses and how they lead to the torque that causes the deflection of the rod in the electric field. Here’s a step-by-step solution:
Step 1: Understanding the Setup
We have two point masses, each of mass m, attached to a massless rigid non-conducting wire of length L. One mass carries a charge of −q and the other carries a charge of +q. When placed in a uniform electric field E, the arrangement will experience forces due to the electric field.
Hint: Visualize the system and identify the forces acting on each charge due to the electric field.
Step 2: Calculate the Forces
The force acting on the charge +q is given by:
F+=qE
The force acting on the charge −q is:
F−=−qE
Since the charges are equal in magnitude but opposite in sign, the magnitudes of the forces are the same:
F=qE
Hint: Remember that the direction of the force on the positive charge is in the direction of the electric field, while the force on the negative charge is in the opposite direction.
Step 3: Calculate the Torque
The torque τ about the center of the rod (midpoint) due to these forces can be calculated. The distance from the center to each charge is L2. The torque due to each force is:
τ+=F+⋅L2⋅sin(θ)=qE⋅L2⋅sin(θ)
τ−=F−⋅L2⋅sin(θ)=−(−qE)⋅L2⋅sin(θ)=qE⋅L2⋅sin(θ)
Thus, the total torque is:
τ=τ++τ−=qE⋅L2⋅sin(θ)+qE⋅L2⋅sin(θ)=qELsin(θ)
Hint: Use the fact that torque is the product of force and the perpendicular distance from the pivot point.
Step 4: Moment of Inertia
The moment of inertia I of the system about the center is:
I=2⋅m(L2)2=2⋅m⋅L24=mL22
Hint: Recall that the moment of inertia for point masses is calculated using I=mr2.
Step 5: Relate Torque and Angular Acceleration
Using the relation τ=Iα, we can express the angular acceleration α:
α=τI=qELsin(θ)mL22=2qEsin(θ)mL
Hint: This step connects the torque to the angular motion of the system.
Step 6: Small Angle Approximation
For small angles, sin(θ)≈θ (in radians). Thus:
α≈2qEθmL
Hint: This approximation simplifies the calculations for small deflections.
Step 7: Finding the Time Period
The angular frequency ω can be derived from the equation of motion:
α=−ω2θ
Comparing both expressions gives:
ω2=2qEmL
Thus, the time period T is:
T=2π√Iτ=2π√mL2/2qE=2π√mL2qE
Hint: The time period is the time taken for one complete oscillation.
Step 8: Minimum Time to Align
To find the minimum time to align with the electric field, we consider that it takes T4 to align from an initial angle to the direction of the field:
tmin=T4=14⋅2π√mL2qE=π2√mL2qE
Hint: This step uses the concept of oscillation to determine how quickly the system can align with the field.
Final Solution
The minimum time needed for the rod to align itself along the electric field is:
tmin=π2√mL2qE
We have two point masses, each of mass m, attached to a massless rigid non-conducting wire of length L. One mass carries a charge of −q and the other carries a charge of +q. When placed in a uniform electric field E, the arrangement will experience forces due to the electric field.
The force acting on the charge +q is given by:
F+=qE
The force acting on the charge −q is:
F−=−qE
Since the charges are equal in magnitude but opposite in sign, the magnitudes of the forces are the same:
F=qE
The torque τ about the center of the rod (midpoint) due to these forces can be calculated. The distance from the center to each charge is L2. The torque due to each force is:
τ+=F+⋅L2⋅sin(θ)=qE⋅L2⋅sin(θ)
τ−=F−⋅L2⋅sin(θ)=−(−qE)⋅L2⋅sin(θ)=qE⋅L2⋅sin(θ)
Thus, the total torque is:
τ=τ++τ−=qE⋅L2⋅sin(θ)+qE⋅L2⋅sin(θ)=qELsin(θ)
The moment of inertia I of the system about the center is:
I=2⋅m(L2)2=2⋅m⋅L24=mL22
Using the relation τ=Iα, we can express the angular acceleration α:
α=τI=qELsin(θ)mL22=2qEsin(θ)mL
For small angles, sin(θ)≈θ (in radians). Thus:
α≈2qEθmL
The angular frequency ω can be derived from the equation of motion:
α=−ω2θ
Comparing both expressions gives:
ω2=2qEmL
Thus, the time period T is:
T=2π√Iτ=2π√mL2/2qE=2π√mL2qE
To find the minimum time to align with the electric field, we consider that it takes T4 to align from an initial angle to the direction of the field:
tmin=T4=14⋅2π√mL2qE=π2√mL2qE
The minimum time needed for the rod to align itself along the electric field is:
tmin=π2√mL2qE
Topper's Solved these Questions
Similar Questions
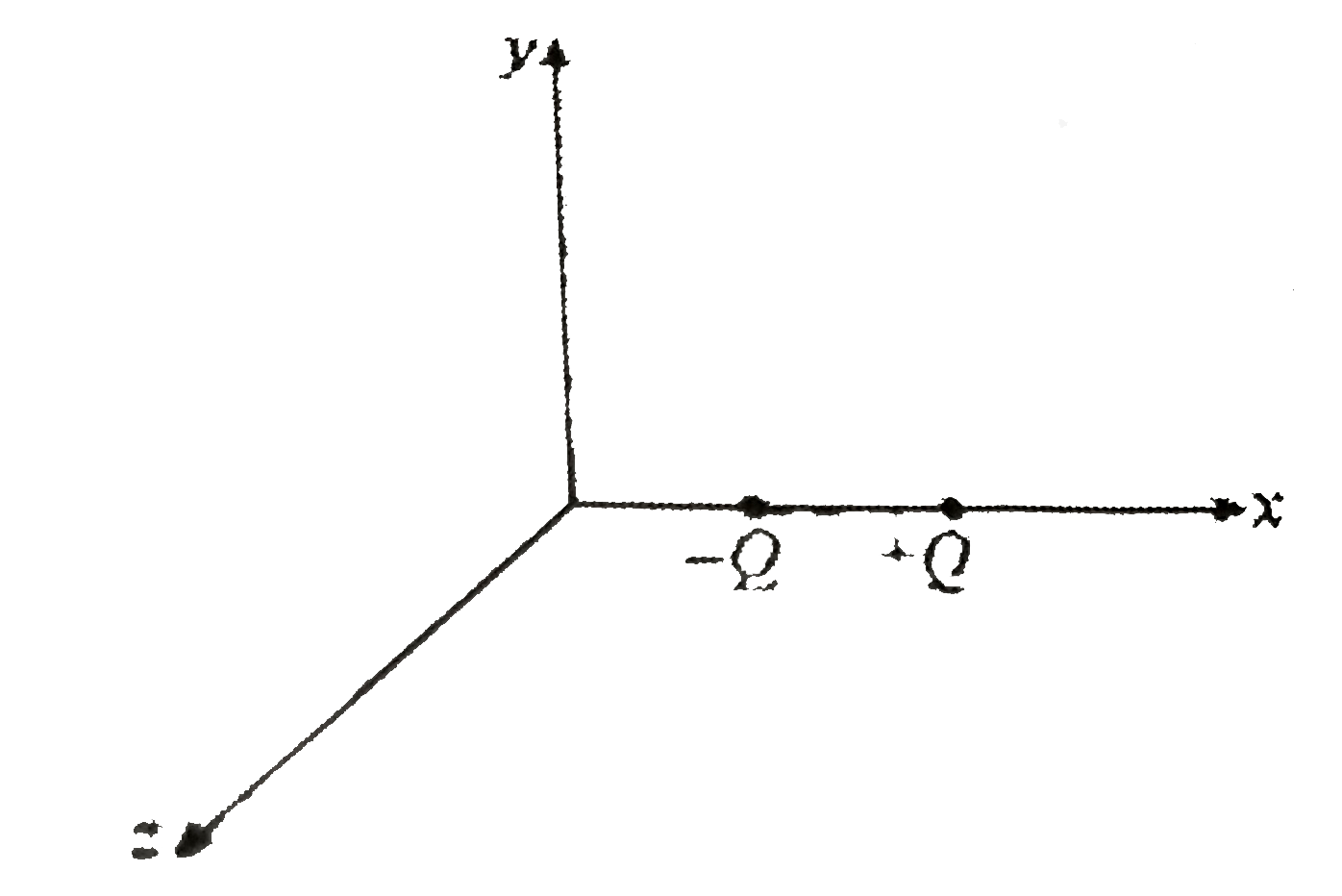
Two small balls of mass Meach carrying charges +Q and −Q, connected by a massless rigid non-conducting rod of length L lie along x-axis as shown. A uniform electric field→E=3ˆk+3ˆj has been switched on. The angular velocity vectorof the dipole when dipole nioment aligns with the electric field is :
View SolutionTwo point masses, m each carrying charges −q and +q are attached to the ends of a massless rigid non - conducting wire of length L. When this arrangement is placed in a uniform electric field, then it deflects through an angle θ. The minimum time needed by the rod to align itself along the field is
View Solution
Knowledge Check
A particle of mass 'm' and charge 'q' is suspended from the ceiling with the help of an insulating wire of length 'l'. It is placed in an uniform electric field as shown in figure. Then the time period of oscillation is
_2019_CBT6_E01_041_Q01.png) A ⎷l√g2+(qEm)2B2π ⎷l√g2+(qEm)2C2π ⎷l√g2+(qEm)D2π ⎷l√g2−(qEm)2
A ⎷l√g2+(qEm)2B2π ⎷l√g2+(qEm)2C2π ⎷l√g2+(qEm)D2π ⎷l√g2−(qEm)2Two masses each of mass M are attached to the end of a rigid massless rod of length L. The moment of interia of the system about an axis passing centre of mass and perpendicular to its length is.
AML24BML22CML2D2ML2A particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
Aq2EyBqEyCaE2yDqEy2
Two point masses of mass m and equal and opposite charge of magnitude q are attached on the corners of a non-conducting uniform rod of mass m and the system is released from rest in uniform electric field E as shown in figure from θ=53∘

(i) Find angular acceleration of the rod just after releasing
(ii) What will be angular velocity of the rod when it passes through stable equilibrium.
(iii) Find work required to rotate the system by 180∘.
View SolutionA bar magnet of length 2 l and magnetic moment m is suspended freely in a uniform magnet field B. Find the amount of work done to deflect the magnet through an angle θ from the direction of the field.
View SolutionA point particle of mass M is attached to one end of a massless rigid non-conducting rod of length L. Another point particle of the same mass is attached to the other end of the rod. The two particles carry charges +q and −q respectively. This arrangement is held in a region of a uniform electric field E such that the rod makes a small angle θ (say of about 5 degree) with the field direction, fig. Find an expression for the minimum time needed for the rod to become parrallel to the field after it is set free.

View SolutionTwo particles, carrying charges -q and +q and having equal masses m each, are fixed at the rod is clamped at an end and is placed in a uniform electric field E with the axis of the dipole along the electric field. The rod is slightly tlted and then released. Neglecting gravity find the time period of small oscillations.
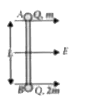
View SolutionTwo small balls A and B of positive charge Q each and masses m and 2m respectively are connected by a non conducting light rod of length L. This system is released in a uniform electric field of strength E as shown. Just after the release (assume no other force acts on the system)
View Solution

