A variable line through the point (65,65) cuts the coordinate axes at the points A and B respectively. If the point P divides AB internally in the ratio 2:1, then the equation of the locus of P is
5xy=(2x+y)
5xy=2(2x+y)
5xy=(x+2y)
5xy=2(x+2y)
The correct Answer is:B
To solve the problem, we need to find the locus of point P that divides the line segment AB in the ratio 2:1, where A and B are the points where a variable line through the point (65,65) intersects the x-axis and y-axis, respectively.
1. Identify Points A and B:
- Let the line cut the x-axis at point A, which has coordinates A(a,0).
- Let the line cut the y-axis at point B, which has coordinates B(0,b).
2. Equation of the Line:
- The equation of the line in intercept form is given by:
xa+yb=1
- Since the line passes through the point (65,65), we can substitute these coordinates into the equation:
65a+65b=1
- Multiplying through by 5ab gives:
6b+6a=5ab
- Rearranging this, we get:
1a+1b=56
3. Coordinates of Point P:
- Point P divides AB in the ratio 2:1. Using the section formula, the coordinates of P (h,k) are given by:
h=1⋅a+2⋅01+2=a3
k=1⋅0+2⋅b1+2=2b3
4. Expressing a and b in terms of h and k:
- From h=a3, we find:
a=3h
- From k=2b3, we find:
b=3k2
5. Substituting a and b into the equation:
- Substitute a and b into the equation 1a+1b=56:
13h+23k=56
- Multiply through by 6hk to eliminate the denominators:
2k+4h=5hk
- Rearranging gives:
5hk−2k−4h=0
6. Final Locus Equation:
- Rearranging the above equation:
5hk−2k=4h
- Factoring out k:
k(5h−2)=4h
- Thus, the locus of point P is:
k=4h5h−2
Final Equation:
- The final equation of the locus of point P can be expressed as:
2y+4x=5xy
or equivalently,
5xy−2y−4x=0
- Let the line cut the x-axis at point A, which has coordinates A(a,0).
- Let the line cut the y-axis at point B, which has coordinates B(0,b).
- The equation of the line in intercept form is given by:
xa+yb=1
- Since the line passes through the point (65,65), we can substitute these coordinates into the equation:
65a+65b=1
- Multiplying through by 5ab gives:
6b+6a=5ab
- Rearranging this, we get:
1a+1b=56
- Point P divides AB in the ratio 2:1. Using the section formula, the coordinates of P (h,k) are given by:
h=1⋅a+2⋅01+2=a3
k=1⋅0+2⋅b1+2=2b3
- From h=a3, we find:
a=3h
- From k=2b3, we find:
b=3k2
- Substitute a and b into the equation 1a+1b=56:
13h+23k=56
- Multiply through by 6hk to eliminate the denominators:
2k+4h=5hk
- Rearranging gives:
5hk−2k−4h=0
- Rearranging the above equation:
5hk−2k=4h
- Factoring out k:
k(5h−2)=4h
- Thus, the locus of point P is:
k=4h5h−2
- The final equation of the locus of point P can be expressed as:
2y+4x=5xy
or equivalently,
5xy−2y−4x=0
Topper's Solved these Questions
Similar Questions
A variable line through the point (65,65) cuts the coordinates axes in the point AandB. If the point P divides AB internally in the ratio 2:1, show that the equation to the locus of P is : 5xy=2(2x+y).
View SolutionA variable line through the point (15,15)cuts the coordinate axes in the points A and B. If the point P divides AB internally in the ratio 3:1, then the locus of P is (A) 3x+y=20xy (B) y+3x=20xy (C) x+y=20xy (D) 3x+3y=20xy
View Solution
Knowledge Check
Let a variable line passing through a fixed point P in the first quadrant cuts the positive coordinate axes at points A and B respectively. If the area of ΔOAB is minimum, then OP is
AAltitude through vertex O of ΔAOBBMedian through vertex O of ΔAOBCInternal angle bisector through vertex O of ΔAOBDNone of these
A straight line through the point A(1,1) meets the parallel lines 4x+2y=9 & 2x+y+6=0 at points P and Q respectively. Then the point A divides the segment PQ in the ratio:
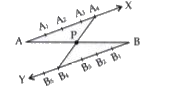
View SolutionFrom the following figure, point P divides AB internally in the ratio ________.
View SolutionFind the equation of straight line which passes through the point P(2,6) and cuts the coordinate axis at the point A and B respectively so that AP:BP=2:3.
View SolutionA(2,3) is a fixed point and Q(3cosθ,2sinθ) a variable point. If P divides AQ internally in the ratio 3:1, find the locus of P.
View SolutionWrite the coordinates of the point dividing line segment joining points (2, 3) and (3, 4) internally in the ratio 1 :5 .
View SolutionWrite the coordinates ot the point dividing line segment joining the points (1, 5) and (-5,1) internally in the ratio 1: 4.
View SolutionCalculate the co-ordinates of the point P that divides the line joining point A(−1,3) and B(5,−6) internally in the ratio 1:2
View Solution
