In an experiment, a boy plots a graph between for a simple pendulum for different values of (small) amplitudes, where and is the maximum velocity and the maximum acceleration respectively. He found the graph to be a straight line with a negative slope, making an angle of when the experiment was conducted on the earth surface. When the same experiment was conducted at a height h above the surface, the line was at an angle of . The value of h is [radius of the earth = R]
0.5R
0.24R
0.73R
R
The correct Answer is:C
To solve the problem, we need to analyze the relationship between the maximum velocity vmax and the maximum acceleration amax of a simple pendulum at different heights above the Earth's surface.
1. Understanding the Pendulum Motion:
- For a simple pendulum, the maximum velocity vmax and the maximum acceleration amax can be expressed in terms of the amplitude A and the angular frequency ω:
vmax=Aω
amax=−Aω2
2. Expressing in Terms of Gravity:
- The angular frequency ω is given by:
ω=√gL
- Therefore, we can express vmax and amax as:
vmax=A√gL
amax=−A(gL)
3. Plotting the Graph:
- The graph is plotted between v2max and a2max:
v2max=A2gL
a2max=A2(gL)2
- Thus, the relationship can be simplified to:
v2max=gL⋅a2max
4. Finding the Slope:
- The slope of the line in the graph is given by:
slope=v2maxa2max=1ω2
- When the angle is 30∘ at the Earth's surface:
tan(30∘)=1√3⇒1ω2=1√3⇒ω2=√3
5. At Height h:
- When the experiment is conducted at height h, the angle becomes 60∘:
tan(60∘)=√3⇒1ω2h=√3⇒ω2h=13
6. Relating the Two Conditions:
- The gravitational acceleration g changes with height:
gh=gs1+hR
- Therefore, we can relate ω2 at height h to that at the surface:
ω2h=ghL=gsL(1+hR)
- Setting the two expressions for ω2:
gsL(1+hR)=13
7. Solving for h:
- Rearranging gives:
1+hR=3⇒hR=2⇒h=2R
Final Answer:
The value of h is 0.73R.
- For a simple pendulum, the maximum velocity vmax and the maximum acceleration amax can be expressed in terms of the amplitude A and the angular frequency ω:
vmax=Aω
amax=−Aω2
- The angular frequency ω is given by:
ω=√gL
- Therefore, we can express vmax and amax as:
vmax=A√gL
amax=−A(gL)
- The graph is plotted between v2max and a2max:
v2max=A2gL
a2max=A2(gL)2
- Thus, the relationship can be simplified to:
v2max=gL⋅a2max
- The slope of the line in the graph is given by:
slope=v2maxa2max=1ω2
- When the angle is 30∘ at the Earth's surface:
tan(30∘)=1√3⇒1ω2=1√3⇒ω2=√3
- When the experiment is conducted at height h, the angle becomes 60∘:
tan(60∘)=√3⇒1ω2h=√3⇒ω2h=13
- The gravitational acceleration g changes with height:
gh=gs1+hR
- Therefore, we can relate ω2 at height h to that at the surface:
ω2h=ghL=gsL(1+hR)
- Setting the two expressions for ω2:
gsL(1+hR)=13
- Rearranging gives:
1+hR=3⇒hR=2⇒h=2R
The value of h is 0.73R.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In Searl's experiment a graph is plotted between
Aload on hanger and radius of wireBload on hanger and mean value of spherometer screw readingCradius of the wire and spherometer screw readingDnone of theseif the maximum and minimum voltage of AM wave are Vmax and Vmin, respectively then modulation factor
Am=VmaxVmax+VminBm=VminVmax+VminCVmax+VminVmax−VminDVmax−VminVmax+Vmin.In an experiment , to find the loss of energy with respect to time in case of swinging simple pendulum , the graph between (amplitude)2 and time is
A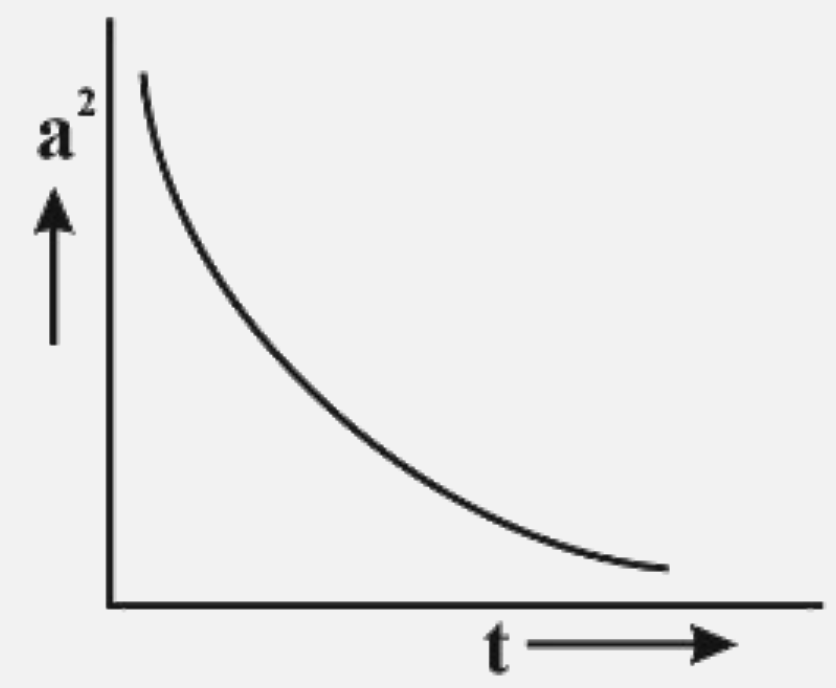 B
B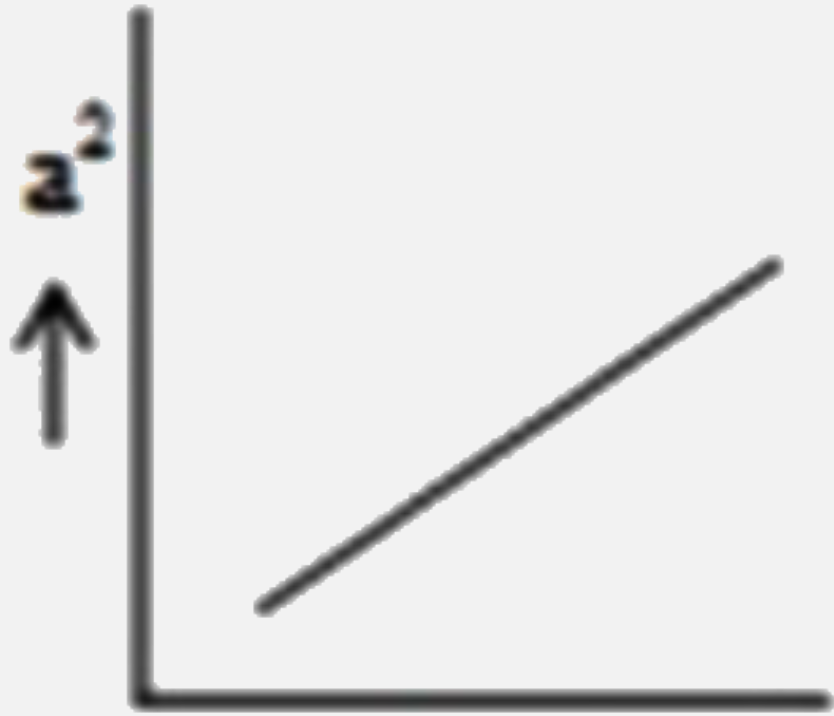 C
C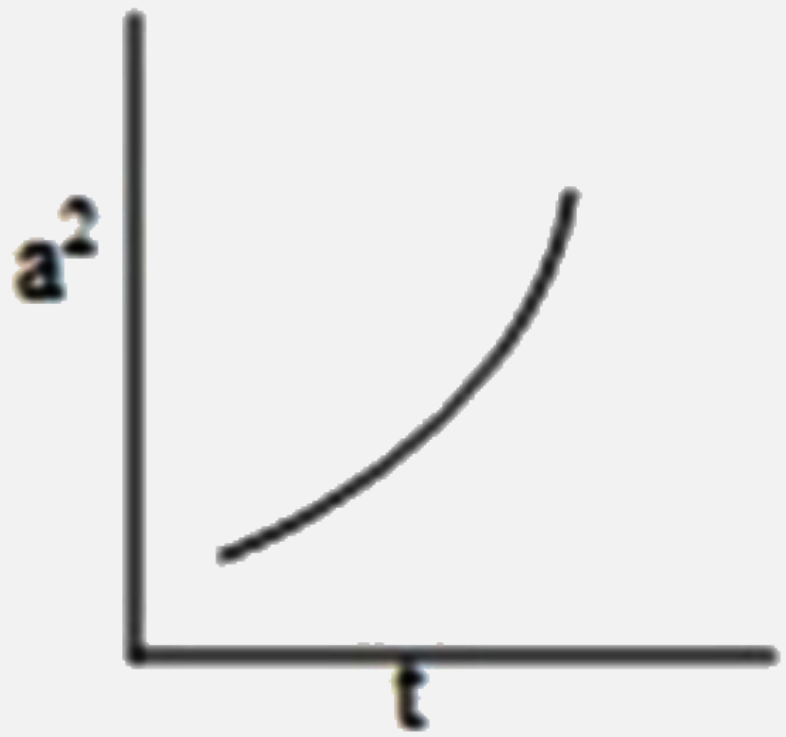 D
D
If the maximum and minimum voltages of an AM wave are Vmax.andVmin. respectively then modulation factor -
View SolutionTwo pendulums oscillates with a constant phase difference of 90∘ and same amplitude. The maximum velocity of one pendulum is v, then the maximum velocity of the other pendulum will be
View SolutionFor e.m. wave propagating along x-axis, Emax=30V/m. What is the maximum value of magnetic field?
View SolutionMax. concentration of Hb normally found in RBC :−
View Solution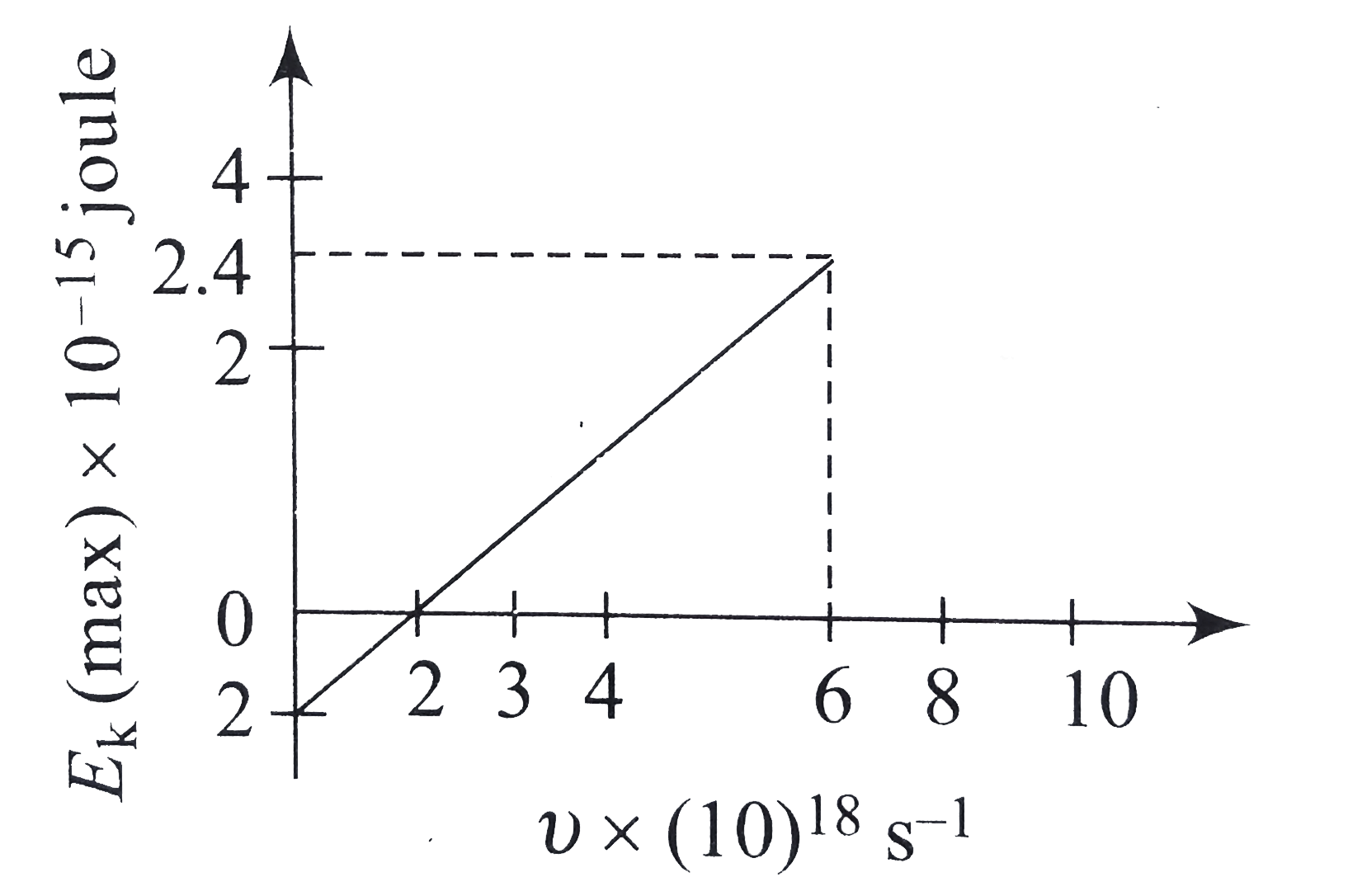
In the experiment on photoelectric effect, the graph between EK(max) and v is found to be a straight line as sshoen in fig. The threshold frequency and Planck's constant according to this graph are
View Solution