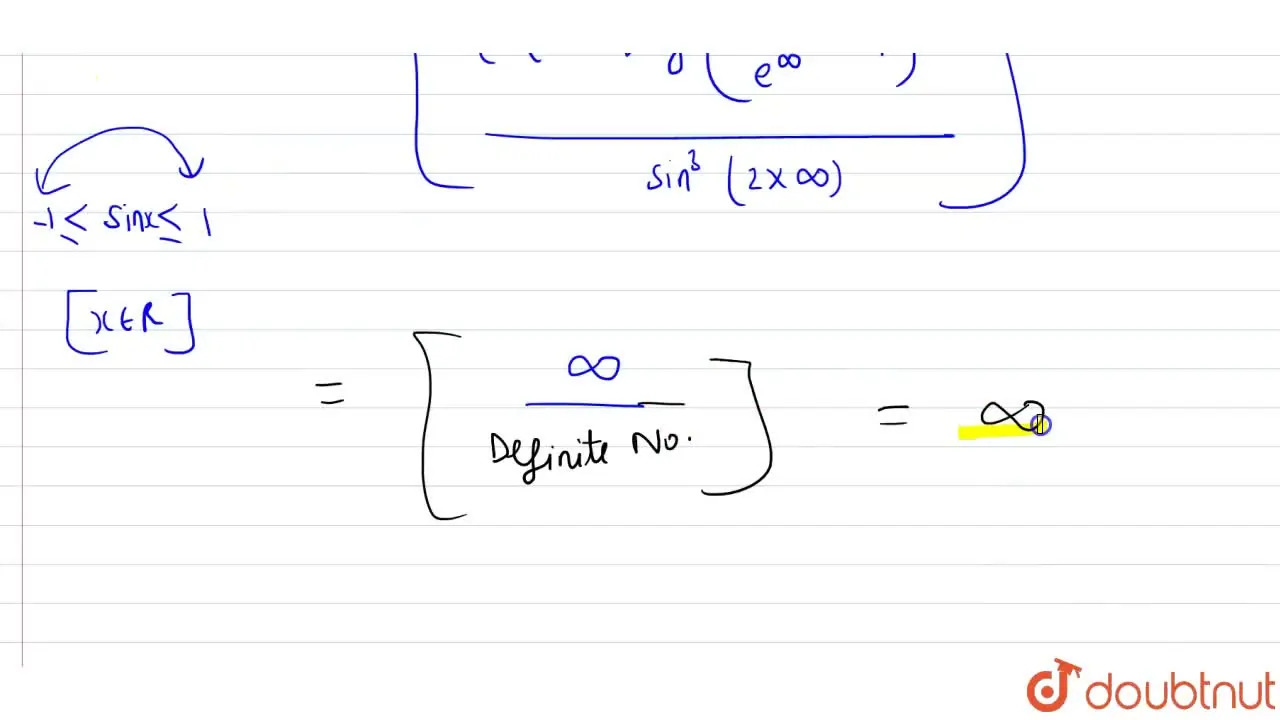
The value of limx→∞ex+1log(x3e−x+1)sin3(2x) is equal to
(Use e = 2.7)
Video Solution
Text Solution
The correct Answer is:0.34
|
Answer
Step by step video, text & image solution for The value of lim_(xrarroo)(e^(x+1)log(x^(3)e^(-x)+1))/(sin^(3)(2x)) is equal to (Use e = 2.7) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Related Playlists
Similar Questions
The value of limx→∞⎡⎢ ⎢⎣e2(1+2x)x⎤⎥ ⎥⎦x2 is equal to
View SolutionThe value of limx→∞(e√x4+−e(x2+1)) is
View SolutionThe value of limx→alog(x−a)log(ex−ea) is
View Solutionthe value of limx→0ex+log(1+x)−(1−x)−2x2
View SolutionThe value of limx→0(ex−x−1)(x−sinx)ln(1+x)x6 is equal to
View SolutionThe value of limx→3(x3+27)loge(x−2)x2−9 is
View SolutionEvaluate: limx→2sin(ex−2−1)log(x−1)
View SolutionThe value of limx→0(1+2x1+3x)1x2.e1ex is
View SolutionThe value of limx→0⎛⎜⎝e1x2−1e1x2+1⎞⎟⎠is :
View Solutionlimx→∞[x−loge(ex+e−x2)]=
View Solution