A voltmeter with a resistance 50×103Ω is used to measure voltage in a circuit. To increase its range to 3 times, the additional resistance to be put in series is
9×106Ω
105Ω
1.5×105Ω
9×105Ω
The correct Answer is:B
To solve the problem, we need to determine the additional resistance required to increase the range of the voltmeter to three times its original measurement capability.
1. Identify the given values:
- Resistance of the voltmeter, Rv=50×103Ω (or 50kΩ).
- We want to increase the voltage range to three times the original, so the new voltage measurement will be 3V.
2. Understanding the relationship:
- The voltage measured by the voltmeter is given by V=I⋅Rv.
- If we add an additional resistance R in series with the voltmeter, the total resistance becomes Rt=Rv+R.
- The new voltage measured will be V′=I⋅Rt=I⋅(Rv+R).
3. Setting up the equation:
- Since we want the new voltage V′ to be three times the original voltage V, we can write:
V′=3V
- Substituting the expressions for V and V′:
I⋅(Rv+R)=3⋅(I⋅Rv)
4. Simplifying the equation:
- We can cancel I from both sides (assuming I≠0):
Rv+R=3Rv
- Rearranging gives:
R=3Rv−Rv=2Rv
5. Calculating the additional resistance:
- Now substitute Rv into the equation:
R=2⋅(50×103)=100×103Ω
- Therefore, the additional resistance required is:
R=100kΩ
Final Answer:
The additional resistance to be put in series is 100kΩ.
---
- Resistance of the voltmeter, Rv=50×103Ω (or 50kΩ).
- We want to increase the voltage range to three times the original, so the new voltage measurement will be 3V.
- The voltage measured by the voltmeter is given by V=I⋅Rv.
- If we add an additional resistance R in series with the voltmeter, the total resistance becomes Rt=Rv+R.
- The new voltage measured will be V′=I⋅Rt=I⋅(Rv+R).
- Since we want the new voltage V′ to be three times the original voltage V, we can write:
V′=3V
- Substituting the expressions for V and V′:
I⋅(Rv+R)=3⋅(I⋅Rv)
- We can cancel I from both sides (assuming I≠0):
Rv+R=3Rv
- Rearranging gives:
R=3Rv−Rv=2Rv
- Now substitute Rv into the equation:
R=2⋅(50×103)=100×103Ω
- Therefore, the additional resistance required is:
R=100kΩ
The additional resistance to be put in series is 100kΩ.
Topper's Solved these Questions
Similar Questions
A voltmeter with resistance 500Omega is used to measure the emf of a cell of internal resistance 4Omega .The percentage error in the reading of the voltmeter will be
View SolutionA voltmeter with resistance 500Ω is used to measure the emf of a cell of internal resistance 4Ω. The percentage error in the reading of the voltmeter will be
View Solution
Knowledge Check
A voltmeter having resistance of 50×103 ohm is used to measure the voltage in a circuit. To increase the range of measurement 3 times the additional series resistance required is
A105 ohmB105 k ohmC900 k ohmD9×106 ohmTo increase the range of voltmeter the series resistance should be
AincreasedBdecreasedCunchangedDnone of theseA voltmeter with resistance 2500Ω indicates a voltage of 125V in the circuit shown in figure. What is the series resistance to be connected ot voltmeter so that it indicates 100V? Consider ideal battery.
 A625ΩB120ΩC550ΩDData are insufficient
A625ΩB120ΩC550ΩDData are insufficient
A voltmeter of resistance 200Ω is used to measure p.d across resistances 100Ω and 200Ω.
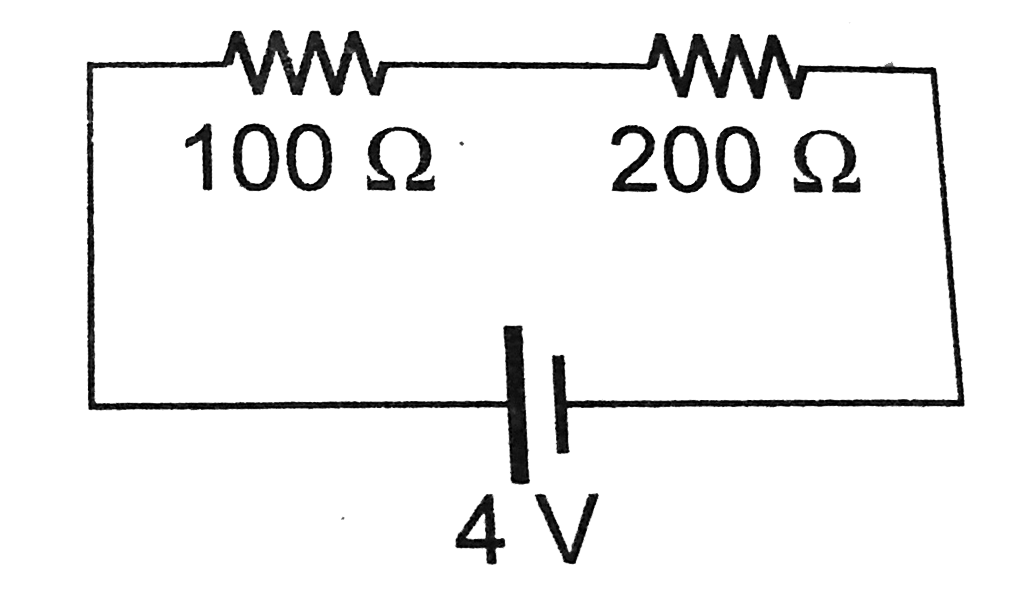 .
.
View SolutionA voltmeter has resistance of 2000 ohms and it can measure upto 2V. If we want ot increase its range to 10V then the, required resistance in series will be
View SolutionResistance of voltmeter is 10000Ω to increase range of voltmeter from 25V, resistance connected in series is
View SolutionA voltmeter with resistance 500Ω is used to measure the emf of a cell of internal resistance 4Ω. The percentage error in the reading of the voltmeter will be
View SolutionA voltmeter has resistance R0 and range V. What resistance should be connected in series with it to increase its range to n V ?
View Solution

