Let D is a point on the line l1:x+y=2=0andS(3,3) is a fixed point. The line l2 is perpendicular to DS and passes through S. If M is another point on the line l1 (other than D), then the locus of the point of intersection of l2 and the angle bisector of the angle MDS is
(x+y−2)2=2(x−3)2+2(y−3)2
(x+y−2)2=(x−2)2+(y−3)2
(x+y−2)2=(x−3)2+(y−3)22
None of these
The correct Answer is:A
To solve the problem step by step, we will follow the logical deductions based on the given conditions.
Step 1: Define the Points and Lines
Let D(x1,y1) be a point on the line l1:x+y−2=0. This means that x1+y1=2.
Let S(3,3) be the fixed point.
Step 2: Determine the Equation of Line l2
The line l2 is perpendicular to the line segment DS and passes through point S.
The slope of line DS can be calculated as:
slope of DS=y1−3x1−3
Thus, the slope of line l2 (being perpendicular) is:
slope of l2=−x1−3y1−3
Using point-slope form, the equation of line l2 is:
y−3=−x1−3y1−3(x−3)
Step 3: Find Another Point M on Line l1
Let M(x2,y2) be another point on line l1. Therefore, we have:
x2+y2−2=0⟹y2=2−x2
Step 4: Determine the Angle Bisector of ∠MDS
The angle bisector of ∠MDS can be determined using the angle bisector theorem. The coordinates of the intersection point of the angle bisector and line l2 will be denoted as P(h,k).
Step 5: Establish the Relationship Between P, D, and S
Since P is on the angle bisector of ∠MDS, we can use the property of angle bisectors. The distances from point P to points D and S must maintain a ratio based on the lengths of segments MD and MS.
Step 6: Use Perpendicular Distances
Let PF be the perpendicular from point P to line l1. Since P lies on the angle bisector, we have:
PF=PS
Using the distance formula, we can express these distances in terms of h and k.
Step 7: Set Up the Equation
The perpendicular distance from point P(h,k) to line l1 is given by:
PF=|h+k−2|√12+12=|h+k−2|√2
The distance PS is:
PS=√(h−3)2+(k−3)2
Step 8: Equate the Distances
Setting the two distances equal gives:
|h+k−2|√2=√(h−3)2+(k−3)2
Step 9: Square Both Sides
Squaring both sides to eliminate the square root yields:
(h+k−2)22=(h−3)2+(k−3)2
Step 10: Simplify the Equation
Expanding both sides and simplifying will yield the locus of point P.
Step 11: Final Locus Equation
After simplification, we arrive at the final equation that represents the locus of point P.
Let D(x1,y1) be a point on the line l1:x+y−2=0. This means that x1+y1=2.
The line l2 is perpendicular to the line segment DS and passes through point S.
slope of DS=y1−3x1−3
Thus, the slope of line l2 (being perpendicular) is:
slope of l2=−x1−3y1−3
y−3=−x1−3y1−3(x−3)
Let M(x2,y2) be another point on line l1. Therefore, we have:
x2+y2−2=0⟹y2=2−x2
The angle bisector of ∠MDS can be determined using the angle bisector theorem. The coordinates of the intersection point of the angle bisector and line l2 will be denoted as P(h,k).
Since P is on the angle bisector of ∠MDS, we can use the property of angle bisectors. The distances from point P to points D and S must maintain a ratio based on the lengths of segments MD and MS.
Let PF be the perpendicular from point P to line l1. Since P lies on the angle bisector, we have:
PF=PS
Using the distance formula, we can express these distances in terms of h and k.
The perpendicular distance from point P(h,k) to line l1 is given by:
PF=|h+k−2|√12+12=|h+k−2|√2
The distance PS is:
PS=√(h−3)2+(k−3)2
Setting the two distances equal gives:
|h+k−2|√2=√(h−3)2+(k−3)2
Squaring both sides to eliminate the square root yields:
(h+k−2)22=(h−3)2+(k−3)2
Expanding both sides and simplifying will yield the locus of point P.
After simplification, we arrive at the final equation that represents the locus of point P.
Topper's Solved these Questions
Similar Questions
The line l1 passing through the point (1,1) and the 'l2' passes through the point (−1,1) If the difference of the slope of lines is 2. Find the locus of the point of intersection of the l1 and l2
View SolutionIn the xy plane, the line L1 passes through the point (1,1) and the line L2 passes through the point (−1,1). If the difference of the slopes of the lines is 2. Then the locus of the point of intersection of the lines L1andL2 is
View Solution
Knowledge Check
Let D is a point on the line l1:x+y−2=0,S(3,3) is a fixed point and line l2 is the perpendicular to DS and passing through S. If MK is another point on the line l1 (other than D), then the locus of the point of intersection of l2 and angle bisector of the angle MDS is a conic whose length of latus rectus rectum is equal to
A4√2B4C8D2√2Let L be the line passing through the point P (1, 2) such that its intercepted segment between the coordinate axes is bisected at P. If L1 is the line perpendicular to L and passing through the point (−2,1), then the point of intersection of L and L1 is :
A(45,125)B(1120,2910)C(310,175)D(35,2310)Let L be the line passing through the point P (1,2) such that its intercepted segment between the co-ordinate axes is bisected at P. If L1 is the line perpendicular to L and psssing through the point (-2,1), then the point of intersection of L and L1 is
A(45,125)B(35,2310)C(1120),(2910)D(310,175)
Let a given line l1 intersect the X andy - axes at P and Q respectively.Let another line L2,perpendicular to L1, cut the X and Y -axes at R and S, respectively.Show that the locus of the point of intersection of the line PS and QR is a circle passing through the origin.
View SolutionIf the line l - is perpendicular to the line which is passing through the points (6,3),(−2,4) then the slope of l is
View SolutionLet a given line L1 intersect the X and Y axes at P and Q respectively. Let another line L2 perpendicular to L1 cut the X and Y-axes at Rand S, respectively. Show that the locus of the point of intersection of the line PS and QR is a circle passing through the origin
View SolutionLet a line L1:3x+2y−6=0 intersect the x and y axes at P and Q respectively. Let another line L2 perpendicular to L1 cut the x and y axes at R and S respectively.The locus of point of intersection of the lines PS and QR is
View SolutionTwo straight lines l1 and l2 cross each other ar point P The line l1 is moving at a speed v1 perpendicular to itself & line l2 is moving at a speed v2 in the similar fashion. The speed of point P is :
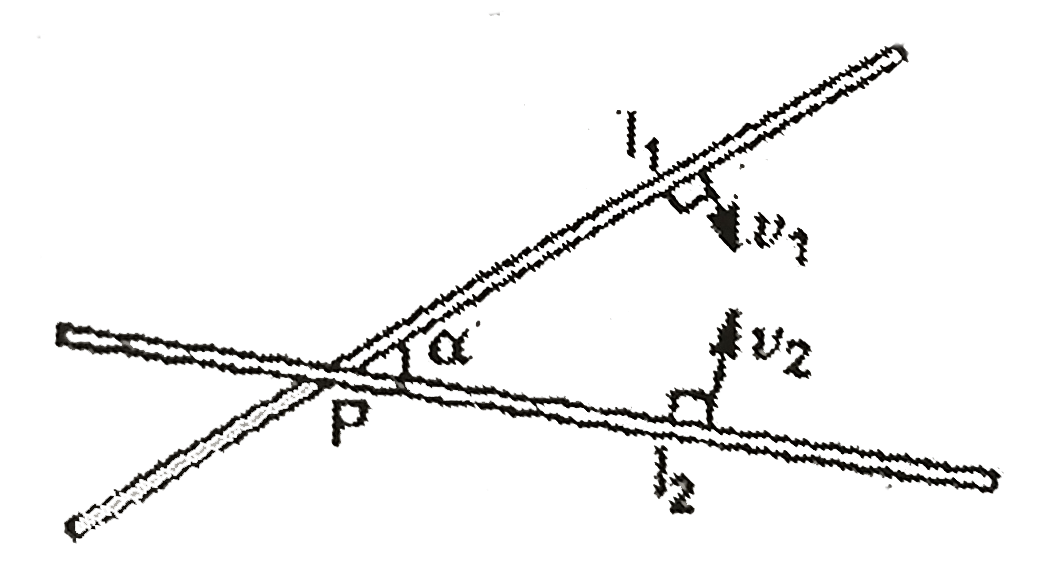
View Solution
