A small particle of mass m and charge Q is dropped in uniform horizontal magnetic field B. The maximum vertical displacement of particle is given by h=nm2g2Q2B2 . Find the value n.
The correct Answer is:4
To solve the problem, we need to analyze the motion of a charged particle in a uniform magnetic field while it is also under the influence of gravity. Here's a step-by-step solution:
Step 1: Understand the Forces Acting on the Particle
When the particle of mass m and charge Q is dropped, it experiences two forces:
1. Gravitational force Fg=mg acting downwards.
2. Magnetic force Fm=Q(v×B), which acts perpendicular to both the velocity v of the particle and the magnetic field B.
Step 2: Analyze the Motion
The particle will experience a downward acceleration due to gravity and a magnetic force that causes it to move in a circular path in the horizontal plane. The motion will not be purely circular because of the downward gravitational force.
Step 3: Set Up the Equations of Motion
We can break down the motion into horizontal (x-direction) and vertical (y-direction) components. The magnetic force will cause the particle to have a horizontal component of velocity.
1. In the x-direction, the magnetic force provides the centripetal force necessary for circular motion.
2. The vertical motion is influenced by gravity.
Step 4: Use Energy Conservation
At the maximum height h, the particle's vertical velocity becomes zero. We can use energy conservation to relate the potential energy at height h to the kinetic energy it had when it was dropped.
- Potential Energy at height h: PE=mgh
- Kinetic Energy in the horizontal direction: KE=12mv2x
At the maximum height, we have:
mgh=12mv2x
From this, we can express vx:
vx=√2gh
Step 5: Relate Magnetic Force and Acceleration
The magnetic force acting on the particle can also be expressed as:
Fm=QvB
This force provides the necessary centripetal acceleration for the circular motion in the horizontal plane.
Step 6: Integrate the Forces
Using the relation between the forces, we can express the maximum vertical displacement h in terms of the given quantities:
h=nm2g2Q2B2
Step 7: Compare and Solve for n
From the analysis, we find that:
h=4m2g2Q2B2
Thus, comparing with the given formula:
nm2g2Q2B2=4m2g2Q2B2
This implies that:
n=4
Final Answer
The value of n is 4.
---
When the particle of mass m and charge Q is dropped, it experiences two forces:
1. Gravitational force Fg=mg acting downwards.
2. Magnetic force Fm=Q(v×B), which acts perpendicular to both the velocity v of the particle and the magnetic field B.
The particle will experience a downward acceleration due to gravity and a magnetic force that causes it to move in a circular path in the horizontal plane. The motion will not be purely circular because of the downward gravitational force.
We can break down the motion into horizontal (x-direction) and vertical (y-direction) components. The magnetic force will cause the particle to have a horizontal component of velocity.
2. The vertical motion is influenced by gravity.
At the maximum height h, the particle's vertical velocity becomes zero. We can use energy conservation to relate the potential energy at height h to the kinetic energy it had when it was dropped.
- Kinetic Energy in the horizontal direction: KE=12mv2x
mgh=12mv2x
From this, we can express vx:
vx=√2gh
The magnetic force acting on the particle can also be expressed as:
Fm=QvB
This force provides the necessary centripetal acceleration for the circular motion in the horizontal plane.
Using the relation between the forces, we can express the maximum vertical displacement h in terms of the given quantities:
h=nm2g2Q2B2
From the analysis, we find that:
h=4m2g2Q2B2
Thus, comparing with the given formula:
nm2g2Q2B2=4m2g2Q2B2
This implies that:
n=4
The value of n is 4.
Topper's Solved these Questions
Similar Questions
A particle of mass m and charge q is projected into a region having a perpendicular magnetic, field B. Find the angle of deviation of the particle as it comes out of the magnetic field if th,, width of the region is (b)
(a) 2mvBq(b)(mv)/(Bq)(c)(mv)/(2 Bq)
View SolutionA very small particle of mass m and charge q is given an initial speed u against uniform electric field E. How much distance will the particle cover before acquiring the same speed again?
View Solution
Knowledge Check
A particle of mass m and charge q is thrown in a region where uniform gravitational field and electric field are present. The path of particle:
Astraight lineBellipseCparabolaDcircleA charged particle of mass m and charge q describes circular motion of radius r in a uniform magnetic field of strength B. The frequency of revolution is
A3Bq2πmB3Bq2πmC2πm2BqDBq2πmA particle of mass 'm' and charge 'Q' is acceleration in cyclotron. If magnetic field is 'B' and radius cyclotron is r then find the kinetic energy of particle.
AQBr2mBQ2B2r2mCQ2B2r22mDQ2B2r2m
A charged particle projected in a magnetic field
B=(3ˆi+4ˆj)×10−2T
The acceleration of the particle is found to be
a=(xˆi+2ˆj)ms2
find the value of x
View SolutionA particle of charge q and mass m is prjected in a uniform and contant magnetic field of strength B.The initial velocity →v makes angle θ with the →B.Find the distance travelled by the particle in time t.
View SolutionA charged particle of charge q and mass m enters perpendiculalry in a magnetic field B. Kinetic energy of particle E, then frequency of rotation is
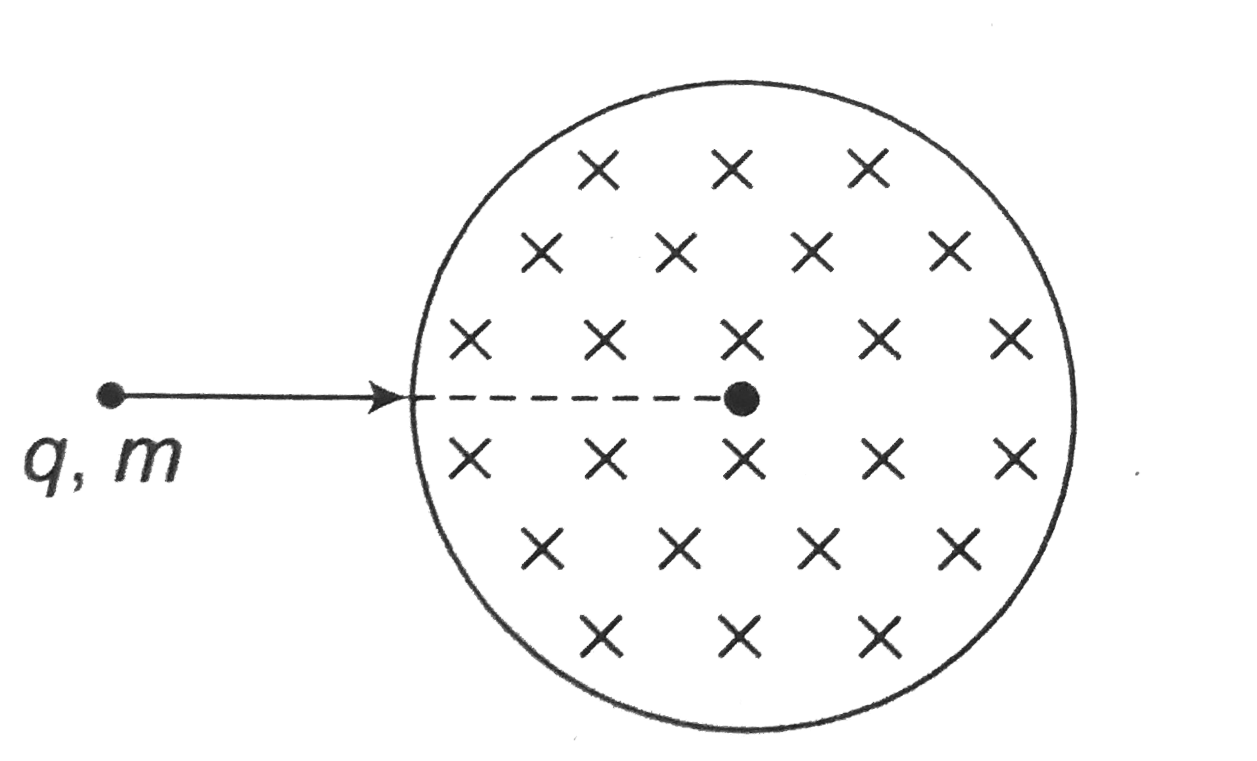
View SolutionA particle having mass m, charge q enters a cylindrical region having uniform magnetic field B in the inward direction as shown. If the particle is deviated by 60∘ as it emerges out of the field then what is the time spent by it in the field?
View SolutionA particle of mass m and charge q enters a magnetic field B perpendicularly with a velocity v, The radius of the circular path described by it will be
View Solution