(i) State Bohr's quantization condition for defining stationary orbits . How does de- Broglie hypothesis explain the stationary orbits ?
(ii) find the relation beween the three wavelengths
λ1,λ2 and λ3 from the energy level diagram shown :

Only those orbits are stable for which the angular momentum of revolving electron is an integral multiple of (h2π) where h is the planck’s constant. Thus the angular momentum (L) of the orbiting electron is quantised. That is L=nh2π
According to dc Broglie hypothesis
Linear momentum =hλ
and for circular orbit
L = rnp, where rn is the radius of quantised
orbits
=rnhλ
Also, L=nh2π
∴rnhλ=nh2π or 2πr=nλ
Hence, circumference of permitted orbits are integral multiples of the wavelength
Topper's Solved these Questions
- CBSE EXAMINATION PAPER - 2016 Book:CBSE COMPLEMENTARY MATERIALChapter:CBSE EXAMINATION PAPER - 2016 Exercise:SECTION - E
Explore 17 Videos
- CBSE EXAMINATION PAPER - 2016 Book:CBSE COMPLEMENTARY MATERIALChapter:CBSE EXAMINATION PAPER - 2016 Exercise:SECTION - B
Explore 5 Videos
- CBSE BOARD EXAMNATION PAPER (2017 )Book:CBSE COMPLEMENTARY MATERIALChapter:CBSE BOARD EXAMNATION PAPER (2017 )Exercise:SECTION E
Explore 12 Videos
- CBSE Examination Paper Delhi–2014Book:CBSE COMPLEMENTARY MATERIALChapter:CBSE Examination Paper Delhi–2014Exercise:SET-III (Questions Uncommon to set-I and II)
Explore 9 Videos
Similar Questions
(i) State Bohr's quantisation condition for defining stationary orbits. How does de-Broglie hypothesis explain the stationary orbits ?
(ii) Find the relation between the three wavelengths, λ1,λ2 and λ3 from the energy level diagram shown here.
View Solution(i) State Bohr's quantization condition for defining stationary orbits . How does de- Broglie hypothesis explain the stationary orbits ?
(ii) find the relation beween the three wavelengths
λ1,λ2 and λ3 from the energy level diagram shown :

View Solution
Knowledge Check
Some energy levels of a molecule are shown in the fig. The ratio of the wavelengths r=λ1/λ2, is given by
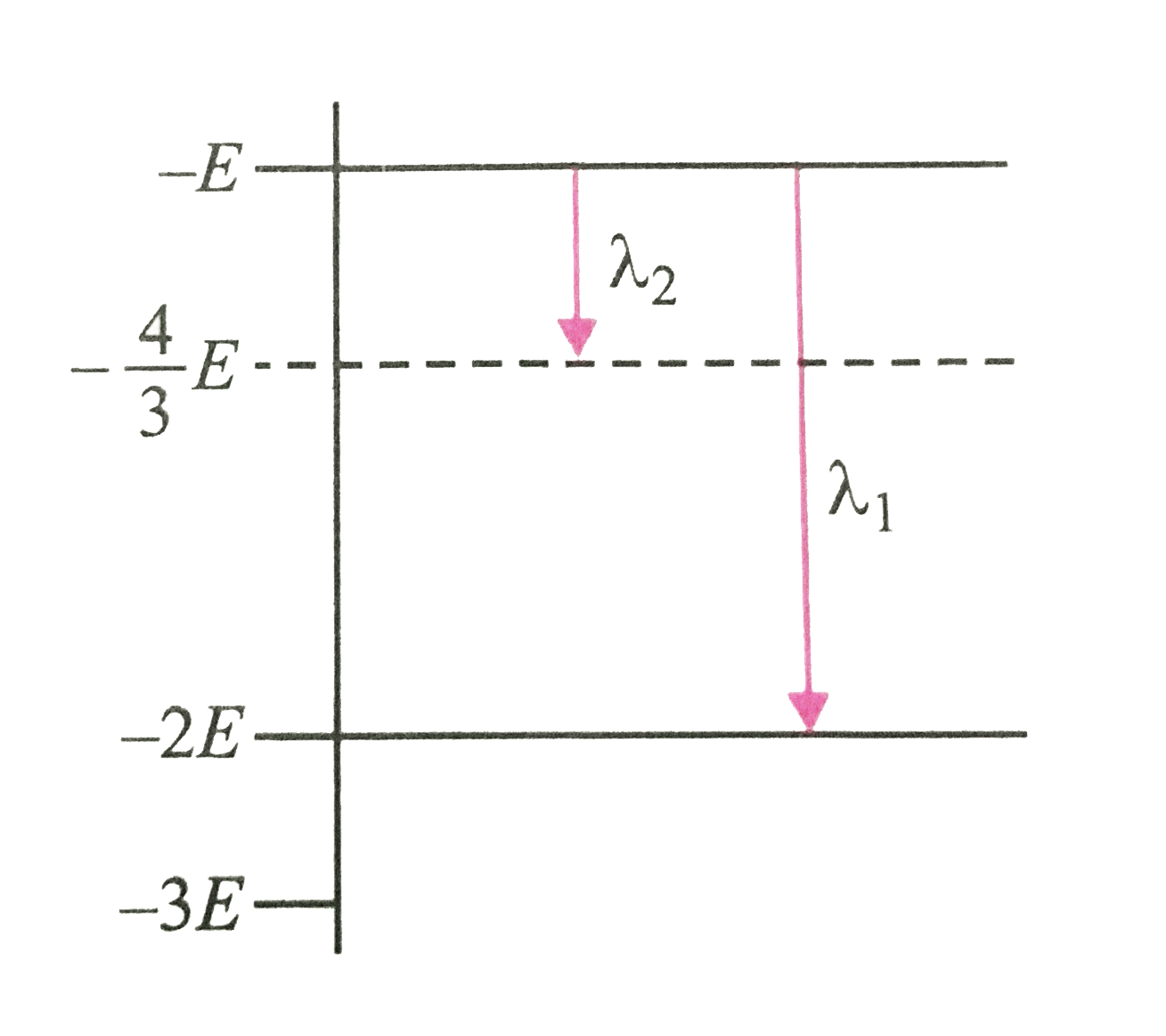 Ar=34Br=13Cr=43Dr=23
Ar=34Br=13Cr=43Dr=23Some energy levels of a molecule are shown in the figure. The ratio of the wavelengths r=λ1/λ2 is given by -
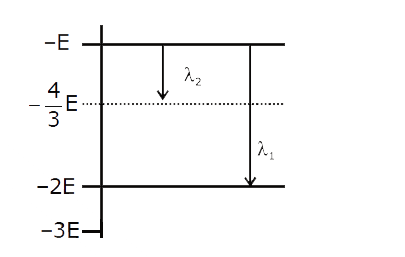 Ar=13Br=43Cr=23Dr=34
Ar=13Br=43Cr=23Dr=34An electron is moving in Bohr's fourth orbit. Its de Broglie wavelength is λ. What is the circumference of the fourth orbit?
A2/λB2λC3λD3/λ
Find the relation between the three wavelengths λ1,λ2andλ3 from the energy level diagram shown below.
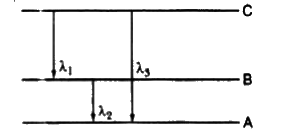
View SolutionState Bohr's quantum condition for stationary orbits in terms of de-Broglie wavelength.
View Solution(a) State Bohr's postulate to define stable orbits in hydrogen atom. How does de Broglie's hypothesis explain the stability of these orbits ?
(b) A hydrogen atom initially in the ground state absorbs a photon which excites it to then n = 4 level . Estimate the frequeny of the photon.
View Solution(a) State Bohr's postulate to define stable orbits in hydrogen atom. How does de Broglie's hypothesis explain the stability of these orbits ?
(b) A hydrogen atom initially in the ground state absorbs a photon which excites it to then n = 4 level . Estimate the frequeny of the photon.
View Solution(a) State Bohr's postulate to define stable orbits in hydrogen atom. How does de-Broglie's hypothesis explain the stability of these orbits ?
(b) A hydrogen atom initially in the ground state absorbs a photon which excites it to the p=4 level. Estimale the frequency of the pholon.
View Solution