A cell of emf ‘E’ and internal resistance ‘r’ is connected across a variable load resistor R. Draw the terminal voltage V versus (i) R and (ii) the current l.
It is found that when R=4Ω, the current is 1 A and when R is increased to 9Ω, the current reduce to 0.5 A. Find the values of the emf E and internal resistance r.
To solve the problem, we need to find the values of the emf E and internal resistance r of the cell based on the given conditions. Let's break down the solution step by step.
Step 1: Understanding the Circuit
The terminal voltage V of a cell is given by the equation:
V=E−I⋅r
where:
- E is the emf of the cell,
- I is the current flowing through the circuit,
- r is the internal resistance of the cell.
Step 2: Setting Up the Equations
We have two scenarios provided in the question:
1. When R=4Ω, the current I=1A.
2. When R=9Ω, the current I=0.5A.
Using Ohm's law, we can express the current in terms of E, r, and R:
I=ER+r
Step 3: Formulating the First Equation
For the first scenario (R=4Ω, I=1A):
1=E4+r
Rearranging gives us:
E=1(4+r)(Equation 1)
E=4+r
Step 4: Formulating the Second Equation
For the second scenario (R=9Ω, I=0.5A):
0.5=E9+r
Rearranging gives us:
E=0.5(9+r)(Equation 2)
E=4.5+0.5r
Step 5: Equating the Two Equations
Now we have two expressions for E:
1. E=4+r
2. E=4.5+0.5r
Setting them equal to each other:
4+r=4.5+0.5r
Step 6: Solving for r
Rearranging the equation:
r−0.5r=4.5−4
0.5r=0.5
r=1Ω
Step 7: Finding E
Now substituting r back into Equation 1 to find E:
E=4+r=4+1=5V
Final Values
Thus, the values we found are:
- E=5V
- r=1Ω
Summary of Steps:
1. Write the equation for terminal voltage.
2. Set up equations based on the two scenarios.
3. Rearrange to find expressions for E.
4. Equate the two expressions for E.
5. Solve for r.
6. Substitute r back to find E.
The terminal voltage V of a cell is given by the equation:
V=E−I⋅r
where:
- E is the emf of the cell,
- I is the current flowing through the circuit,
- r is the internal resistance of the cell.
We have two scenarios provided in the question:
1. When R=4Ω, the current I=1A.
2. When R=9Ω, the current I=0.5A.
I=ER+r
For the first scenario (R=4Ω, I=1A):
1=E4+r
Rearranging gives us:
E=1(4+r)(Equation 1)
E=4+r
For the second scenario (R=9Ω, I=0.5A):
0.5=E9+r
Rearranging gives us:
E=0.5(9+r)(Equation 2)
E=4.5+0.5r
Now we have two expressions for E:
1. E=4+r
2. E=4.5+0.5r
4+r=4.5+0.5r
Rearranging the equation:
r−0.5r=4.5−4
0.5r=0.5
r=1Ω
Now substituting r back into Equation 1 to find E:
E=4+r=4+1=5V
Thus, the values we found are:
- E=5V
- r=1Ω
1. Write the equation for terminal voltage.
2. Set up equations based on the two scenarios.
3. Rearrange to find expressions for E.
4. Equate the two expressions for E.
5. Solve for r.
6. Substitute r back to find E.
Topper's Solved these Questions
- CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)Book:CBSE COMPLEMENTARY MATERIALChapter:CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)Exercise:SECTION E
Explore 6 Videos
- CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)Book:CBSE COMPLEMENTARY MATERIALChapter:CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)Exercise:SECTION B
Explore 6 Videos
- CBSE Examination Paper Delhi–2014Book:CBSE COMPLEMENTARY MATERIALChapter:CBSE Examination Paper Delhi–2014Exercise:SET-III (Questions Uncommon to set-I and II)
Explore 9 Videos
- DUAL NATURE OF MATTER AND RADIATION & ATOMS AND NUCLEIBook:CBSE COMPLEMENTARY MATERIALChapter:DUAL NATURE OF MATTER AND RADIATION & ATOMS AND NUCLEIExercise:Long Answer Question
Explore 22 Videos
Similar Questions
A cell of emf ‘E’ and internal resistance ‘r’ is connected across a variable load resistor R. Draw the terminal voltage V versus (i) R and (ii) the current l.
It is found that when R=4Ω, the current is 1 A and when R is increased to 9Ω, the current reduce to 0.5 A. Find the values of the emf E and internal resistance r.
View SolutionA cell of emf ε and internal resistance 'r' is connected across a variable load resistor 'R'. Draw the plots of the terminal voltage 'V' versus (i) R and (ii) the current I.
It is found that when R = 4 Ω , the current is 1 A and when R is increased to 9 Ω , the current reduces to 0.5 A. Find the values of the emf ε and internal resistance r.
View Solution
Knowledge Check
A cell of emf 'E' and internal resistance 'r' is connected to a variable external resistor 'R'. The graph which gives the terminal voltage of cell 'V' with respect to R is :
A B
B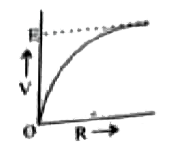 C
C D
D
A cell of emf (E) and internal resistance r is connected across a variable external resistance . R. The graph of terminal potential difference V as a function of R is
A B
B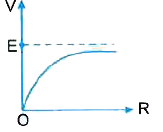 C
C D
D
A cell of emf ε and internal resistance r is charged by a current I, then
Athe cell stores chemical energy at the rate of εiBthe cell stores chemical energy at the rate of i2rCthe cell stores chemical energy at the rate of εI−i2rDthe storage of chemical energy rate cannot be calculated
.A cell of emf E and internal resistance r is connected across a variable resistor. Plot a graph showing variation of terminal voltage V of cell versus the current.
View SolutionA cell of emf ε and internal resistance r is connected across a variable load resistance R. It is found that when R=4Ω the current is 1A and when R is increased to 9Ω, the current reduces to 0.5A. Find the value of the emf ε and internal resistancer
View SolutionA cell of emf 'E' and internal resistance 'r' draws a current 'I'. Write the relation between terminal voltage 'V' in terms of E, I and r.
View SolutionA battery of emf E and internal resistance r is connected to a variable resistor R as shown in figure. Which one of the following is true ?

View SolutionA cell of internal resistance r connected across an external resistance R can supply maximum current when
View Solution