What is the electric flux through a cube of side 1 cm which encloses an electric dipole ?

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem of finding the electric flux through a cube of side 1 cm that encloses an electric dipole, we can follow these steps:
1. Understanding the Problem:
- We have a cube with a side length of 1 cm.
- Inside this cube, there is an electric dipole, which consists of two equal and opposite charges (a positive charge +q and a negative charge -q).
2. Applying Gauss's Law:
- Gauss's Law states that the electric flux (Φ) through a closed surface is equal to the net charge (Q) enclosed by that surface divided by the permittivity of free space (ε₀):
$Φ = \frac{Q_{enc}}{ϵ_{0}}$
3. Calculating the Net Charge:
- In the case of an electric dipole, the total charge enclosed by the cube is:
$Q_{enc} = + q + (- q) = 0$
- Therefore, the net charge inside the cube is zero.
4. Finding the Electric Flux:
- Substituting the net charge into Gauss's Law:
$Φ = \frac{0}{ϵ_{0}} = 0$
- This means that the electric flux through the cube is zero.
5. Conclusion:
- The electric flux through the cube that encloses the electric dipole is:
$Φ = 0 {N m}^{2} / C$

Updated on:7/8/2024

The electric flux through the surface

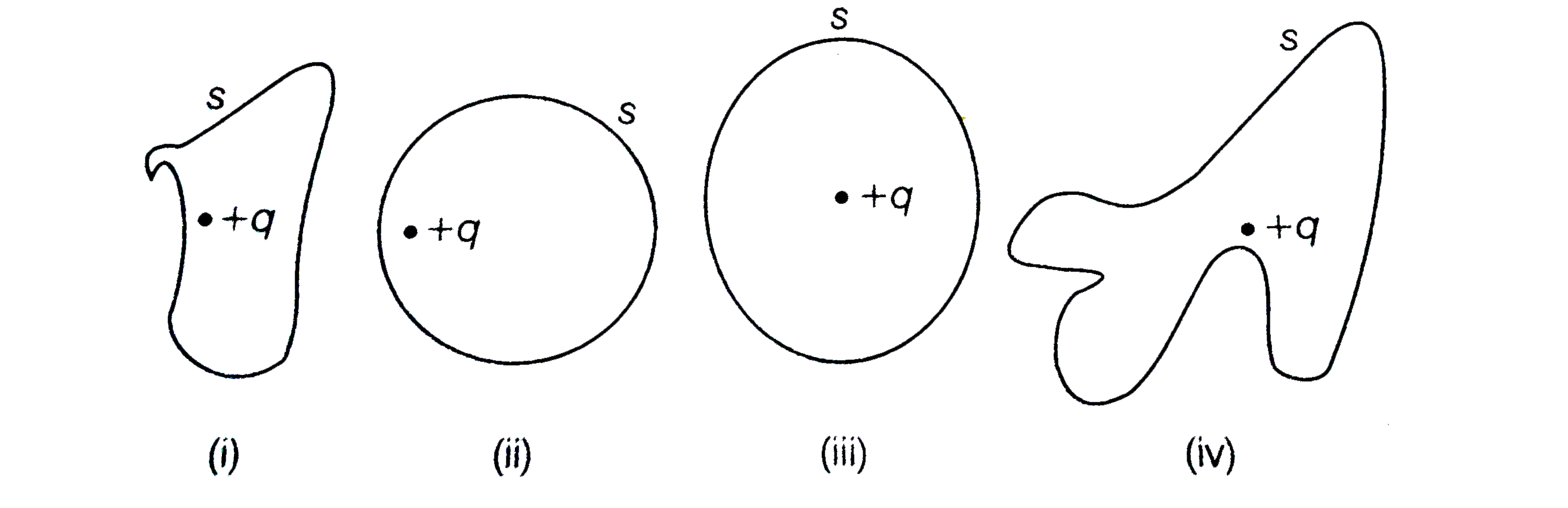Ain fig. (iv) is the largest
Bin fig. (iii) is the least
Cin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)
DIs the same for all the figures.
The electric flux through the surface

Ain fig, (iv) is the largest
Bin fig, (iii) is the least
Cin fig (ii) is same as a fig (iii) but is smaller than that in Fig (iv).
Dis the same for all the figures.
Electric flux through a cube with charge q inside is
A $\frac{q}{ε_{0}}$
B $\frac{q}{6 ε_{0}}$
C $\frac{q}{3 ε_{0}}$
D0