A mass M splits into two parts m and (M-m), which are separated by a cetain distance. The ratio m/M which maximizes the gravitational force between the parts is
1:4
1:3
1:2
1:1
The correct Answer is:C
To solve the problem of finding the ratio mM that maximizes the gravitational force between two parts of a mass M split into m and M−m, we can follow these steps:
Step 1: Write the expression for gravitational force
The gravitational force F between two masses m and M−m separated by a distance r is given by Newton's law of gravitation:
F=G⋅m⋅(M−m)r2
where G is the gravitational constant.
Step 2: Rewrite the force in terms of m
The expression can be rewritten as:
F=G⋅(mM−m2)r2
Step 3: Differentiate the force with respect to m
To find the value of m that maximizes the force, we need to take the derivative of F with respect to m and set it to zero:
dFdm=Gr2⋅(M−2m)
Step 4: Set the derivative equal to zero
Setting the derivative equal to zero gives:
M−2m=0
Step 5: Solve for m
From the equation M−2m=0, we can solve for m:
2m=M⟹m=M2
Step 6: Find the ratio mM
Now, we can find the ratio mM:
mM=M2M=12
Conclusion
Thus, the ratio mM that maximizes the gravitational force between the two parts is:
mM=12
---
The gravitational force F between two masses m and M−m separated by a distance r is given by Newton's law of gravitation:
The expression can be rewritten as:
To find the value of m that maximizes the force, we need to take the derivative of F with respect to m and set it to zero:
Setting the derivative equal to zero gives:
From the equation M−2m=0, we can solve for m:
Now, we can find the ratio mM:
Thus, the ratio mM that maximizes the gravitational force between the two parts is:
Topper's Solved these Questions
- GRAVITATIONBook:CBSE COMPLEMENTARY MATERIALChapter:GRAVITATIONExercise:NUMERICALS
Explore 10 Videos
- DIMENSIONS AND MEASUREMENT Book:CBSE COMPLEMENTARY MATERIALChapter:DIMENSIONS AND MEASUREMENT Exercise:M.C.Q PHYSICAL WORLD & MEASUREMENT
Explore 20 Videos
- KINEMATICSBook:CBSE COMPLEMENTARY MATERIALChapter:KINEMATICSExercise:M.C.Q.
Explore 20 Videos
Similar Questions
Mass M is split into two parts m and (M−m), which are then separated by a certain distance. What is the ratio of (m/M) which maximises the gravitational force between the parts ?
View SolutionA mass M is split into two parts m and (M-m) which are then separated by certain distance. Find ratio (m/M) to maximise the gravitational force F=Gm(M−m)r2 between the parts.
Here G = gravitational constant and r is the distance between m and (M-m).
View Solution
Knowledge Check
A mass M splits into two parts m and (M - m) , which are then separated by a certain distance. Wha ratio (m/M) maximize the gravitational force between the path ?
A23B34C12D13A mass M at rest is broken into two pieces having masses m and (M-m). The two masses are then separated by a distance r. The gravitational force between them will be maximum when the ratio of the masses [m : (M-m) of the two parts is
A1:1B1:2C1:3D1:4Mass M=1 unit is divided into two parts X and (1−X). For a given separation the value of X for which the gravitational force between them becomes maximum is
A1/2B3/5C1D2
Mass M is divided into two parts m1, and m2, For a given separation the ratio of m1M for which the gravitational attraction between the two parts becomes maximum is
View SolutionMass M is divided into two parts x M and (1-x)M. For a given separation, the value of x for which the gravitational attraction between the two pieces becomes maximum is
View SolutionA mass M is broken into two parts of masses m1 and m2. How are m1 and m2 related so that force of gravitational attraction between the two parts is maximum?
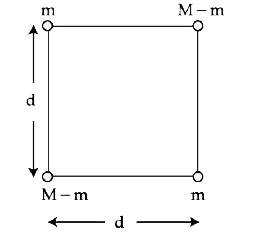
View SolutionA body of mass (2M) splits into four masses {m,M−m,m,M−m}, which are rearranged to form a square as shown in the figure. The ratio of Mm for which, the gravitational potential energy of the system becomes maximum is x : 1 . The value of x is ________.
View SolutionThe gravitational force between two particles of masses m1 and m2 separeted by the same distance, then the gravitational force between them will be
View Solution

