A block slides down as incline of 60∘ with the horizontal. Starting from rest, it covers 8 m in the first 2 seconds. Find the coefficient of static friction
To solve the problem of finding the coefficient of static friction for a block sliding down an incline of 60∘ that covers 8 m in the first 2 seconds, we can follow these steps:
Step 1: Identify the given data
- Angle of incline, θ=60∘
- Distance covered, s=8m
- Time taken, t=2s
- Initial velocity, u=0m/s (starting from rest)
Step 2: Use the equation of motion to find acceleration
We can use the equation of motion:
s=ut+12at2
Substituting the known values:
8=0⋅2+12a(22)
This simplifies to:
8=2a⟹a=82=4m/s2
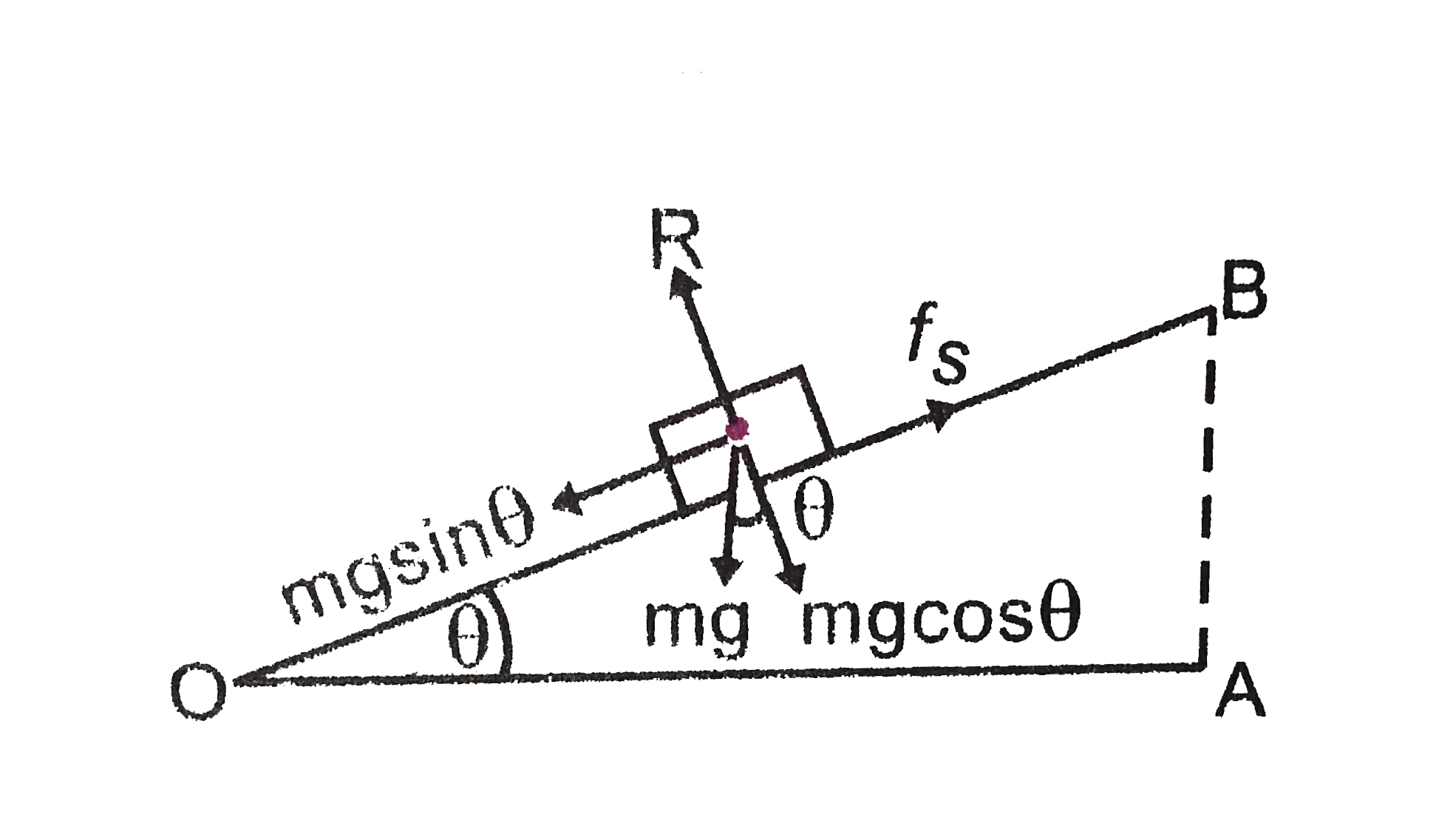
Step 3: Analyze the forces acting on the block
The forces acting on the block are:
1. The gravitational force, mg
2. The normal force, R
3. The frictional force, Fs
The gravitational force can be resolved into two components:
- Parallel to the incline: mgsinθ
- Perpendicular to the incline: mgcosθ
Step 4: Set up the equation of motion along the incline
Using Newton's second law along the incline:
mgsinθ−Fs=ma
Where Fs is the static friction force, which can be expressed as:
Fs=μR=μmgcosθ
Substituting this into the equation gives:
mgsinθ−μmgcosθ=ma
Step 5: Simplify the equation
Dividing through by m (mass of the block):
gsinθ−μgcosθ=a
Rearranging gives:
μgcosθ=gsinθ−a
Thus:
μ=gsinθ−agcosθ
Step 6: Substitute the known values
Using g=9.8m/s2, sin60∘=√32, and cos60∘=12:
μ=9.8⋅√32−49.8⋅12
Calculating the numerator:
9.8⋅√32≈8.487(using √3≈1.732)
So:
μ=8.487−44.9=4.4874.9≈0.914
Step 7: Final calculation
Calculating the final value:
μ≈0.914
Conclusion
The coefficient of static friction, μ, is approximately 0.914.
---
- Angle of incline, θ=60∘
- Distance covered, s=8m
- Time taken, t=2s
- Initial velocity, u=0m/s (starting from rest)
We can use the equation of motion:
s=ut+12at2
Substituting the known values:
8=0⋅2+12a(22)
This simplifies to:
8=2a⟹a=82=4m/s2
The forces acting on the block are:
1. The gravitational force, mg
2. The normal force, R
3. The frictional force, Fs
- Parallel to the incline: mgsinθ
- Perpendicular to the incline: mgcosθ
Using Newton's second law along the incline:
mgsinθ−Fs=ma
Where Fs is the static friction force, which can be expressed as:
Fs=μR=μmgcosθ
Substituting this into the equation gives:
mgsinθ−μmgcosθ=ma
Dividing through by m (mass of the block):
gsinθ−μgcosθ=a
Rearranging gives:
μgcosθ=gsinθ−a
Thus:
μ=gsinθ−agcosθ
Using g=9.8m/s2, sin60∘=√32, and cos60∘=12:
μ=9.8⋅√32−49.8⋅12
Calculating the numerator:
9.8⋅√32≈8.487(using √3≈1.732)
So:
μ=8.487−44.9=4.4874.9≈0.914
Calculating the final value:
μ≈0.914
The coefficient of static friction, μ, is approximately 0.914.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBook:CBSE COMPLEMENTARY MATERIALChapter:NEWTON'S LAWS OF MOTIONExercise:5 Marks Questions
Explore 2 Videos
- NEWTON'S LAWS OF MOTIONBook:CBSE COMPLEMENTARY MATERIALChapter:NEWTON'S LAWS OF MOTIONExercise:Laws Of Motion
Explore 20 Videos
- NEWTON'S LAWS OF MOTIONBook:CBSE COMPLEMENTARY MATERIALChapter:NEWTON'S LAWS OF MOTIONExercise:2 Mark Questions
Explore 14 Videos
- MECHANICAL WAVESBook:CBSE COMPLEMENTARY MATERIALChapter:MECHANICAL WAVESExercise:MCQ
Explore 20 Videos
- PROPERTIES OF MATTERBook:CBSE COMPLEMENTARY MATERIALChapter:PROPERTIES OF MATTERExercise:MULTIPLE CHOICE QUESTIONS (MCQs)
Explore 20 Videos
Similar Questions
A block slides down as incline of 60∘ with the horizontal. Starting from rest, it covers 8 m in the first 2 seconds. Find the coefficient of static friction
View SolutionA block slides down an incline of 30∘ with the horizontal starting from rest it covers 8m in the first two seconds Find the coefficient of kinetic friction between the two .
View Solution
Knowledge Check
Starting from rest , a body slides down at 45∘ inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of friction between the body and the inclined plane is
A0.33B0.25C0.75D0.80
A block slides down an inclined surface of inclination 300 with the horizontal. Starting from rest it covers 8 m in the first two seconds. Find the coefficietn of kinetic friction between the two.
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View SolutionTwo blocks of mass 'm' and 'M, are connect to the ends of a string passing over a pulley. 'M' lies on the plane inclined at an angle θ with the horizontal and 'm' is hanging vertically as shown in Fig. The coefficient of static friction between 'M' and the incline is μs. Find the minimum and maximum value of 'm' so that the system is at rest.

View SolutionA mass of 4 kg rest on a horizontal plane . The plane is gradually inclined until an angle 0=15∘ with the horizontal and the mass just begins to slide . What is the coefficient of static friction between the block and the surface ?
View SolutionA block slides down an incline of angle 30∘ with an acceleration of g/4 Find the coefficient of kinetic friction .
View SolutionA block of mass 8 kg is sliding on a surface inclined at an angle of 45∘ with the horizontal . Calculate the acceleration of the block . The coefficient of friction between the block and surface is 0⋅6 ( Take g = 10m/s2)
View Solution

