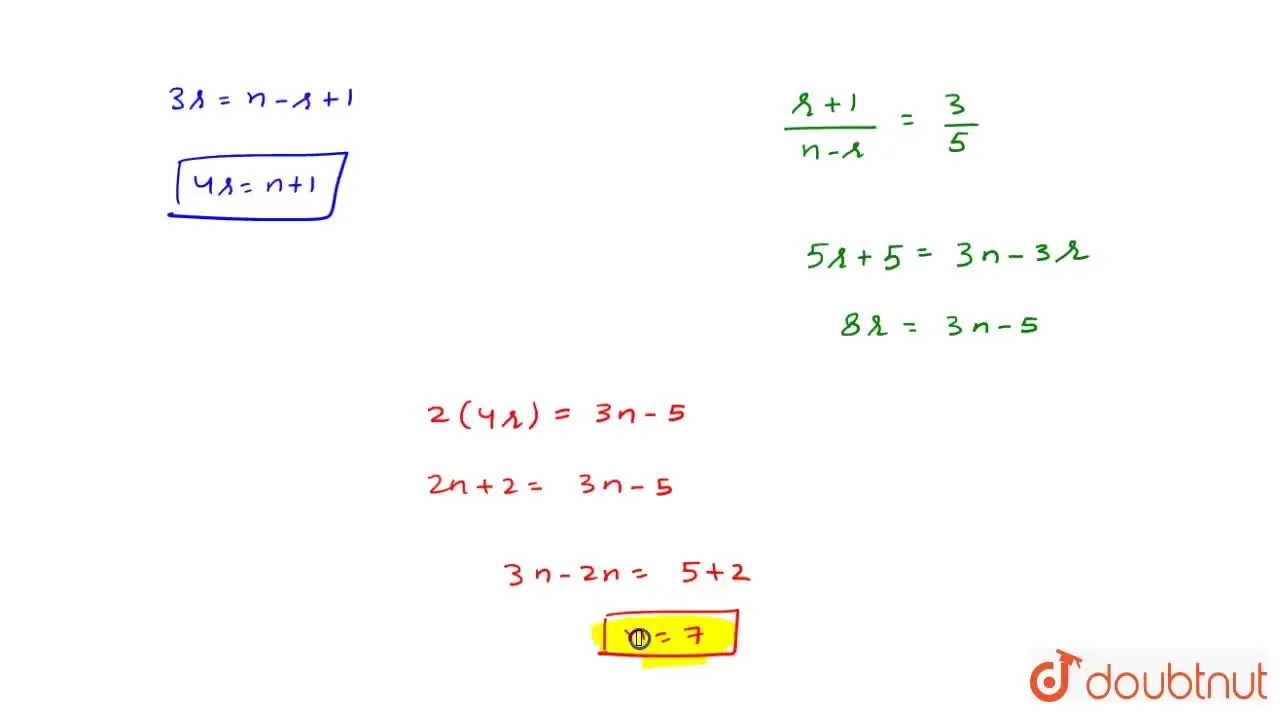
If the coefficients of three consecutive terms in the expansion of (1+x)n are in the ratio 1 : 3 : 5, then show that n = 7.
Step by step video & image solution for If the coefficients of three consecutive terms in the expansion of (1 + x)^(n) are in the ratio 1 : 3 : 5, then show that n = 7. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - BINOMIAL THEOREM EXERCISE - LONG ANSWER TYPE QUESTIONS(Section-D)16videos
BINOMIAL THEOREM
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - BINOMIAL THEOREM EXERCISE - SHORT ANSWER TYPE QUESTIONS((section-B)7videos
BINOMIAL THEOREM
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONS EXERCISE - Short Answer Type Questions49videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
Similar Questions
The coefficients of three consecutive terms in the expansion of (1+x)n are in the ratio 1:7:42. Find n.
View SolutionThe coefficient of three consecutive terms in the expansion of (1+x)nare in the ratio 1 : 6 : 30. Find n.
View SolutionThe coefficients of three consecutive terms in the expansion of (1+a)nare in the ratio 1: 7 : 42. Find n.
View SolutionIf the coefficients of three consecutive terms in the expansion of (1+x)n are in the ratio 1:7:42, then find the value of n.
View SolutionIf the coefficients of three consecutive terms in the expansion of (1+x)n are in the ratio 1:7:42, then find the value of n.
View SolutionIf the coefficients of three consecutive terms in the expansion of (1+x)n are in the ratio 1:7:42, then find the value of n.
View SolutionThe coefficients of three consecutive terms in the expansion of (1+x)n are in the ratio 182:84:30. prove that n=18
View SolutionIf the coefficients of three consecutive terms in the expansion of (1+x)n be 76, 95 and 76 find n.
View SolutionIf for some positive integer n, the coefficients of three consecutive terms in the binomial expansion (1+x)n+5 are in the ratio 5:10:14, then the largest coefficient in this expansion is :
View SolutionWrite the coefficient of the middle term in the expansion of (1+x)2n.
View Solution