How many different products can be obtained by multiplying two or more of the numbers 2, 5, 6, 7, 9 (without repitition)?
The correct Answer is:nC2−n
To find how many different products can be obtained by multiplying two or more of the numbers 2, 5, 6, 7, and 9 (without repetition), we can follow these steps:
Step 1: Identify the numbers
We have the numbers: 2, 5, 6, 7, and 9. There are a total of 5 numbers.
Step 2: Determine combinations for multiplication
We need to find the number of ways to choose 2 or more numbers from these 5 numbers. We will calculate the combinations for choosing 2, 3, 4, and all 5 numbers.
Step 3: Calculate combinations
Using the combination formula nCr=n!r!(n−r)!:
1. Choosing 2 numbers:
5C2=5!2!(5−2)!=5×42×1=10
2. Choosing 3 numbers:
5C3=5!3!(5−3)!=5×42×1=10
3. Choosing 4 numbers:
5C4=5!4!(5−4)!=5
4. Choosing all 5 numbers:
5C5=5!5!(5−5)!=1
Step 4: Sum the combinations
Now, we add all the combinations calculated:
5C2+5C3+5C4+5C5=10+10+5+1=26
Conclusion
Thus, the total number of different products that can be obtained by multiplying two or more of the numbers 2, 5, 6, 7, and 9 is 26.
---
We have the numbers: 2, 5, 6, 7, and 9. There are a total of 5 numbers.
We need to find the number of ways to choose 2 or more numbers from these 5 numbers. We will calculate the combinations for choosing 2, 3, 4, and all 5 numbers.
Using the combination formula nCr=n!r!(n−r)!:
5C2=5!2!(5−2)!=5×42×1=10
5C3=5!3!(5−3)!=5×42×1=10
5C4=5!4!(5−4)!=5
5C5=5!5!(5−5)!=1
Now, we add all the combinations calculated:
5C2+5C3+5C4+5C5=10+10+5+1=26
Thus, the total number of different products that can be obtained by multiplying two or more of the numbers 2, 5, 6, 7, and 9 is 26.
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONS BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Section - D(Long answer type question)
17 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - SECTION-B(Short anwer type question)
11 Videos
- MATHEMATICAL REASONINGBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - MATHEMATICAL REASONINGEXERCISE - SECTION-B SHORT ANSWER TYPE QUESTIONS
5 Videos
- PRACTICE PAPER DESIGN - I BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PRACTICE PAPER DESIGN - I EXERCISE - SECTION -D
6 Videos
Similar Questions
Knowledge Check
How many different four digit numbers can be formed using digits 1, 2, 3, 4, 5, 6, 7, 8, 9 without repetition such that the digit 5 appears exactly once?
A1243B1234C1344D1355How many different four digit numbers can be formed using digits 1, 2, 3, 4, 5, 6, 7, 8, 9 without repetition such that the digit 5 appears exactly once?
A1243B1234C1344D1355How many different four digit numbers can be formed with the digits 1, 2, 3, 4, 5, 6, 7, 8 and 9 such that the digit 5 appears exactly once?
A1024B2048C4096Dnone of these
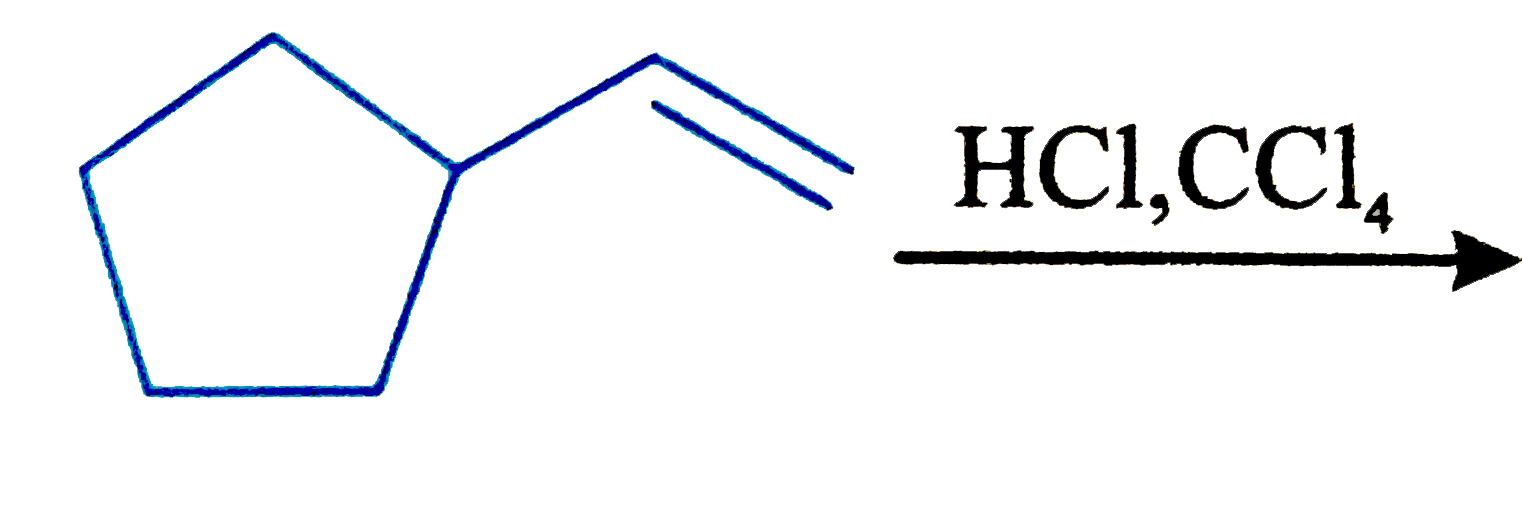
How many different products (exluding stereosiomer) can be obtained by following reaction
View SolutionHow many different 3-digit numbers can be formed by using the digits 0, 2, 5 without repeating any digit in the number?
View SolutionHow many 9-digit numbers of different digits can be formed?
View SolutionThe difference between the greatest and the smallest 5-digit numbers, formed by the digits 0, 3, 6, 7 and 9 without repetition, is:
View SolutionHow many even numbers of 3 different digits can be formed from the digits 1, 2, 3, 4, 5, 6, 7, 8, 9 (repetition of digits is not allowed) ?
View Solution
