State True or False:
A solid ball is exactly fitted inside the cubical box of side a. The volume of the ball is 43πa2
The correct Answer is:F
To determine whether the statement "A solid ball is exactly fitted inside the cubical box of side a. The volume of the ball is 43πa2" is true or false, we will analyze the situation step by step.
1. Understanding the Problem:
- We have a cube with a side length of a.
- A solid ball (sphere) is fitted inside this cube.
2. Identifying the Dimensions:
- The diameter of the sphere will be equal to the side length of the cube, which is a.
- Therefore, the radius r of the sphere can be calculated as:
r=Diameter2=a2
3. Calculating the Volume of the Sphere:
- The formula for the volume V of a sphere is given by:
V=43πr3
- Substituting the radius r=a2 into the volume formula:
V=43π(a2)3
4. Simplifying the Volume Calculation:
- First, calculate (a2)3:
(a2)3=a38
- Now substitute this back into the volume formula:
V=43π⋅a38
- Simplifying this expression:
V=4πa33⋅8=4πa324=πa36
5. Comparing with the Given Statement:
- The statement claims that the volume of the ball is 43πa2.
- We found that the volume of the sphere is πa36.
- Since πa36 is not equal to 43πa2, the statement is false.
Conclusion:
The statement is False.
---
- We have a cube with a side length of a.
- A solid ball (sphere) is fitted inside this cube.
- The diameter of the sphere will be equal to the side length of the cube, which is a.
- Therefore, the radius r of the sphere can be calculated as:
r=Diameter2=a2
- The formula for the volume V of a sphere is given by:
V=43πr3
- Substituting the radius r=a2 into the volume formula:
V=43π(a2)3
- First, calculate (a2)3:
(a2)3=a38
- Now substitute this back into the volume formula:
V=43π⋅a38
- Simplifying this expression:
V=4πa33⋅8=4πa324=πa36
- The statement claims that the volume of the ball is 43πa2.
- We found that the volume of the sphere is πa36.
- Since πa36 is not equal to 43πa2, the statement is false.
The statement is False.
Topper's Solved these Questions
- SURFACE AREA AND VOLUME BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SURFACE AREA AND VOLUME EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS (CHOOSE THE CORRECT ANSWER)
10 Videos
- SURFACE AREA AND VOLUME BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SURFACE AREA AND VOLUME EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
11 Videos
- SURFACE AREA AND VOLUME BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SURFACE AREA AND VOLUME EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS (FILL IN THE BLANKS)
9 Videos
- STATISTICSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STATISTICSEXERCISE - Practice -Test
5 Videos
- TRIANGLEBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - TRIANGLEEXERCISE - Short Answer Type Questions-II
25 Videos
Similar Questions
Knowledge Check
A solid ball of metal has a spherical cavity inside it. The ball is cooled. The volume of the cavity will
AdecreaseBincreaseCreamain sameDhave its shape changedA cubical ball is taken to a depth in volume observed to be 0.1% the bulk modulus of the ball is (g=10m/s2)
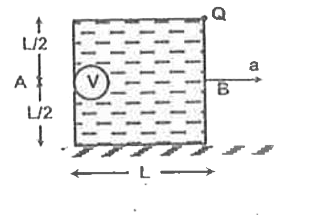
A2×107PaB2×106PaC2×109PaD1.2×109PaA small solid ball of density ρ is held inside at point A of a cubical container of side L, filled with an ideal liquid of density 4ρ as shown in the figure. Now, if the container starts moving with constant acceleration a horizontally and the ball is released from point A simultaneously, then choose from following the correct option(s)
 AFor ball to hit the top of container at end Q,a=3gBFor ball to hit the top of container at end Q,a=2gCBall hits the top of container at end Q after a time t=√L3gDBall hits the top of container at end Q after a time t=√2L3g
AFor ball to hit the top of container at end Q,a=3gBFor ball to hit the top of container at end Q,a=2gCBall hits the top of container at end Q after a time t=√L3gDBall hits the top of container at end Q after a time t=√2L3g
A small ball of volume V and density ρ is held inside a cubical container of side L filled with an ideal liquid of density 4ρ as .Now if the container started moving with constant acceleration a and the ball it hits the top corner point Q of the container . Then find the value of k . Given g=10m/s2
View SolutionA Solid uniform ball of volume V floats on the interface of two immiscible liquids . [The specific gravity of the upper liquid is γ/2 and that of the lower liquid is 2γ, where γ is the specific gravity of the solid ball.] The fraction of the volume of the ball that will be in upper liquid is
View SolutionA solid uniform ball of volume V floats on the interface of two immiscible liquids [The specific gravity of the upper liquid is γ/2 and that of the lower liquid is 2γ, where γ is th especific gracity of the solid ball.] The fraction of the volume of the ball that will be in upper liquid is
View SolutionA box contains 20 balls numbered as 1, 2, 3, …., 20. A ball is drawn at random from the box. What is the probability that the number on the ball is a prime number?
View SolutionIf a radio is purchased for rs. 490 and sold for rs. 465.50. Find the loss %.
View Solution

