In the given Fig., AC is diameter of the circle with centre O and A is point of contact, then find x.
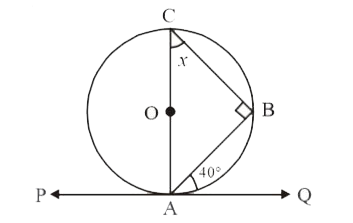
The correct Answer is:x=40∘
Step by step video, text & image solution for In the given Fig., AC is diameter of the circle with centre O and A is point of contact, then find x. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - SHORT ANSWER TYPE - II QUESTIONS
4 Videos
- CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - LONG ANSWER TYPE QUESTIONS
2 Videos
- CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PRACTICE - TEST (SECTION - D)
1 Videos
- ARITHMETIC PROGRESSION BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ARITHMETIC PROGRESSION EXERCISE - PRACTICE TEST (SECTION D)
1 Videos
- Co-ordinate GeometryBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - Co-ordinate GeometryEXERCISE - PRACTICE-TEST (Coordinate Geometry) SECTION-D
1 Videos
Similar Questions
Knowledge Check
In the given figure, AC is the diameter of the circle with centre O. Chord BD is perpendicular to AC. Express p in terms of x.
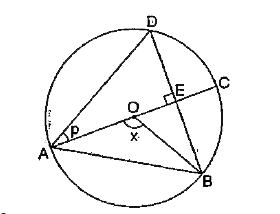 Ax/2B90∘+x/2C90∘−x/2D180∘−x
Ax/2B90∘+x/2C90∘−x/2D180∘−xIn the given figure, O is the centre of the circle. The value of x is
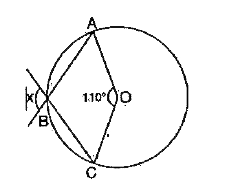 A75∘B55∘C125∘D110∘
A75∘B55∘C125∘D110∘
In the given figure, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ=58∘, find ∠ATQ.
View SolutionIn the given fig, AB is the diameter of the circle with centre O. The point C, D and E are on the circle such that AC = CD = DE = EB. Find ∠EBA.
View SolutionIf Fig , AOB is diameter of a circle with centre O and AC is a tangent to the circle at A . If ∠BOC=130∘ , then find ∠ACO .

View SolutionIn the given fig. OP is equal to the diameter of the circle with centre O. Prove that ΔABP is an equilateral triangle.
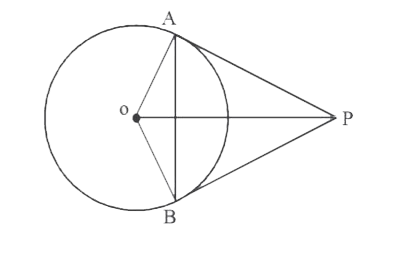
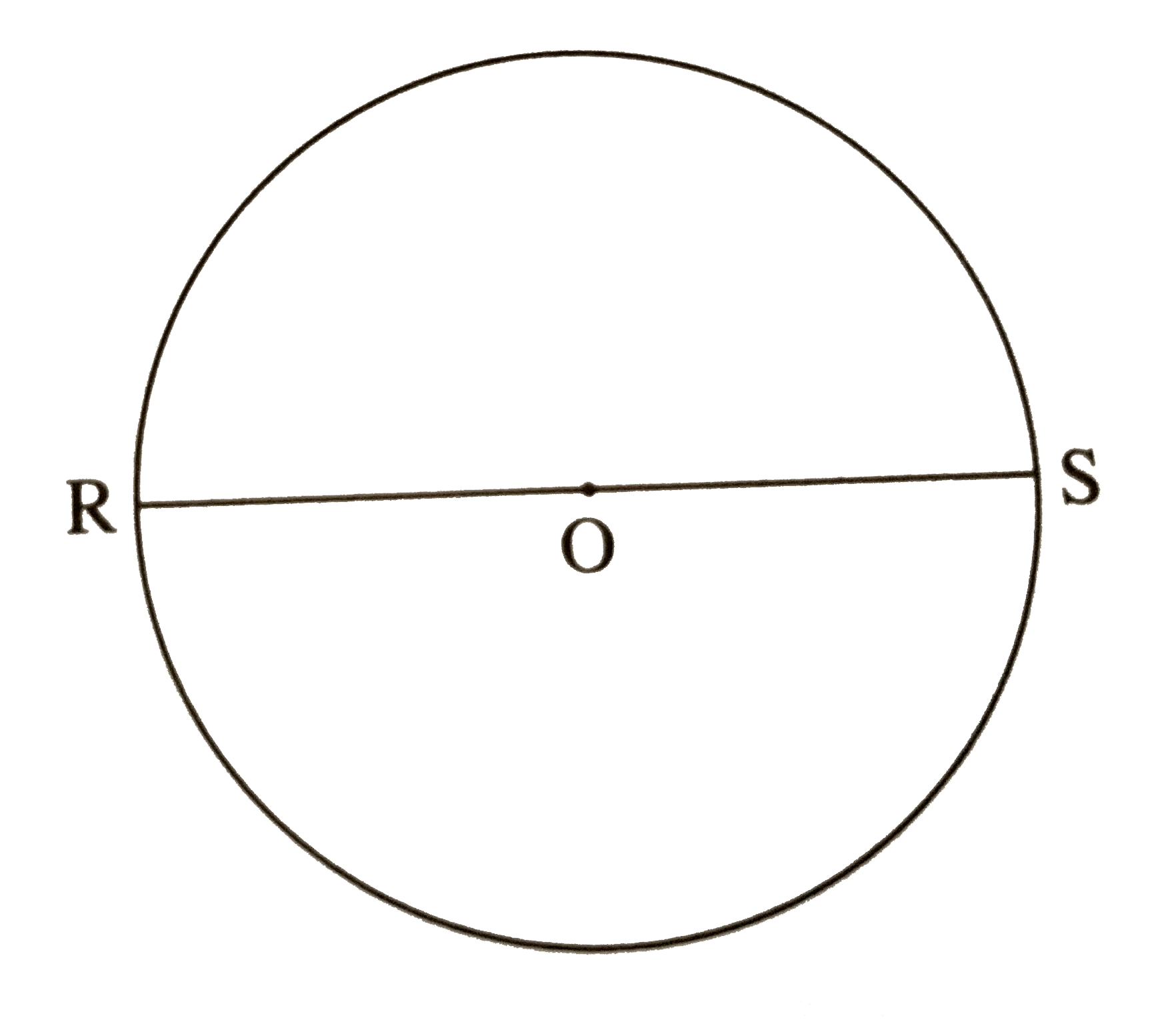
View SolutionIn figure, seg RS is a diameter of the circle with centre O. Point T lines in the exterior of the circle. Prove that ∠RTS is an acute angle.
View SolutionIn the given figure, AB and CD are two diameters of circles ( with centre O) Perpendicular to each other and OD is the diameter of the smallest circle. If OA = 7cm, Find the area of the shaded region.
View Solution