If 10 times of 10th term is equal to 20 times of 20th term of an A.P. Find its 30th term.
The correct Answer is:a30=0
To solve the problem, we need to find the 30th term of an arithmetic progression (A.P.) given that 10 times the 10th term is equal to 20 times the 20th term.
1. Understanding the Terms of A.P.:
The nth term of an A.P. can be expressed as:
An=A+(n−1)d
where A is the first term and d is the common difference.
2. Expressing the 10th and 20th Terms:
- The 10th term (A10):
A10=A+(10−1)d=A+9d
- The 20th term (A20):
A20=A+(20−1)d=A+19d
3. Setting Up the Equation:
According to the problem, we have:
10×A10=20×A20
Substituting the expressions for A10 and A20:
10(A+9d)=20(A+19d)
4. Expanding Both Sides:
- Left-hand side:
10A+90d
- Right-hand side:
20A+380d
Thus, we have:
10A+90d=20A+380d
5. Rearranging the Equation:
Bringing all terms involving A and d to one side:
10A−20A+90d−380d=0
Simplifying this gives:
−10A−290d=0
or
10A+290d=0
6. Finding the Relationship:
Dividing the entire equation by 10:
A+29d=0
This implies:
A=−29d
7. Finding the 30th Term:
The 30th term (A30) can be expressed as:
A30=A+(30−1)d=A+29d
Substituting A=−29d:
A30=−29d+29d=0
Conclusion:
The 30th term of the A.P. is:
0
The nth term of an A.P. can be expressed as:
An=A+(n−1)d
where A is the first term and d is the common difference.
- The 10th term (A10):
A10=A+(10−1)d=A+9d
- The 20th term (A20):
A20=A+(20−1)d=A+19d
According to the problem, we have:
10×A10=20×A20
Substituting the expressions for A10 and A20:
10(A+9d)=20(A+19d)
- Left-hand side:
10A+90d
- Right-hand side:
20A+380d
Thus, we have:
10A+90d=20A+380d
Bringing all terms involving A and d to one side:
10A−20A+90d−380d=0
Simplifying this gives:
−10A−290d=0
or
10A+290d=0
Dividing the entire equation by 10:
A+29d=0
This implies:
A=−29d
The 30th term (A30) can be expressed as:
A30=A+(30−1)d=A+29d
Substituting A=−29d:
A30=−29d+29d=0
The 30th term of the A.P. is:
0
Topper's Solved these Questions
- ARITHMETIC PROGRESSION Book:CBSE COMPLEMENTARY MATERIALChapter:ARITHMETIC PROGRESSION Exercise:SHORT ANSWER TYPE QUESTIONS-II
Explore 17 Videos
- ARITHMETIC PROGRESSION Book:CBSE COMPLEMENTARY MATERIALChapter:ARITHMETIC PROGRESSION Exercise:LONG ANSWER TYPE QUESTIONS
Explore 14 Videos
- ARITHMETIC PROGRESSION Book:CBSE COMPLEMENTARY MATERIALChapter:ARITHMETIC PROGRESSION Exercise:STATE TRUE/FALSE AND JUSTIFY
Explore 5 Videos
- AREAS RELATED TO CIRCLESBook:CBSE COMPLEMENTARY MATERIALChapter:AREAS RELATED TO CIRCLESExercise:PRACTICE-TEST ( AREAS RELATED TO CIRCLES ) SECTION-D
Explore 1 Video
- CIRCLESBook:CBSE COMPLEMENTARY MATERIALChapter:CIRCLESExercise:PRACTICE - TEST (SECTION - D)
Explore 1 Video
Similar Questions
Find the middle term(s) of the A.P. 7, 13, 19, .., 241 .
View SolutionThe sum of the third and the seventh terms of an AP is 6 and their product is 8. Find the sum of first sixteen terms of the AP.
View SolutionIs 301 a term of A.P. 5,11,17,23…….. ?
View SolutionA chord AB of a circle of radius 10 cm makes a right angle at the centre of the circle. Find the area of the major and minor segment. (Use π=3.14)
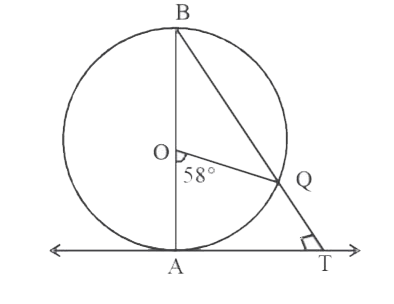
View SolutionAB is a diameter of a circle with centre O and AT is a tangent. If ∠AOQ=58∘ find ∠ATQ.
View Solution(i) 10 times the 10th term and 15 times the 15th term of an A.P. are equal. Find the 25th term of this A.P .
(ii) 17 times the 17th term of an A.P. is equal to 18 times the 18th term. Find the 35th term of this progression.
View Solution(i) 6 times the 6th term of an A.P. is equal to 10 times the 10th term. Prove that its 16th term will be zero.
(ii) 10 times the 10th term of an A.P. is equal to 15 times its 15th term. Find its 25th term.
View Solutionयदि किसी A.P. का 10 वें पद का 10 गुना बराबर हैं 15 वें पद के 15 गुना के , तो दिखायें कि इसका 25 वाँ पद शून्य हैं ।
View Solutionकिसी A.P. के प्रथम 6 पदों का योग 42 हैं तथा इसके 10 वें और 30वें पदों का अनुपात 1:3 हैं । A.P. का पहला और 13 वाँ पद ज्ञात करें ।
View Solution(i ) एक A.P.में 6 वे पद का 6 गुना,,10 वे पद के 10 गुने के बराबर है|सिद्ध कीजिए की इसका 16 वां पद शून्य होगा?
(ii) एक A.P. में 10 वे पद का 10 गुना,15 वे पद के 15 गुने के बराबर है|इसका 25 वां पद ज्ञात कीजिए|
View Solutionयदि किसी समान्तर श्रेढी का 10 वाँ पद 120 तथा 20वाँ पद 110 है तो 200 पदों का योगफल ज्ञात कीजिए ।
View SolutionIf the third term of an A.P. is 12 and 10th term is 26, then its 20th term is :
View SolutionThe sum of the first six terms of an A.P. is 42. The ratio of the 10th term to the 30th term of A.P. is 13 Find the 40th term of the A.P.:
View Solution3rd term of an A.P. Is 12 and 10th term is 26, then its 20th term is :
View SolutionThe sum of first 6 terms of an A.P. is 42. If its 10th and 30th terms are in the ratio 1 : 3, find a8anda12.
View Solution