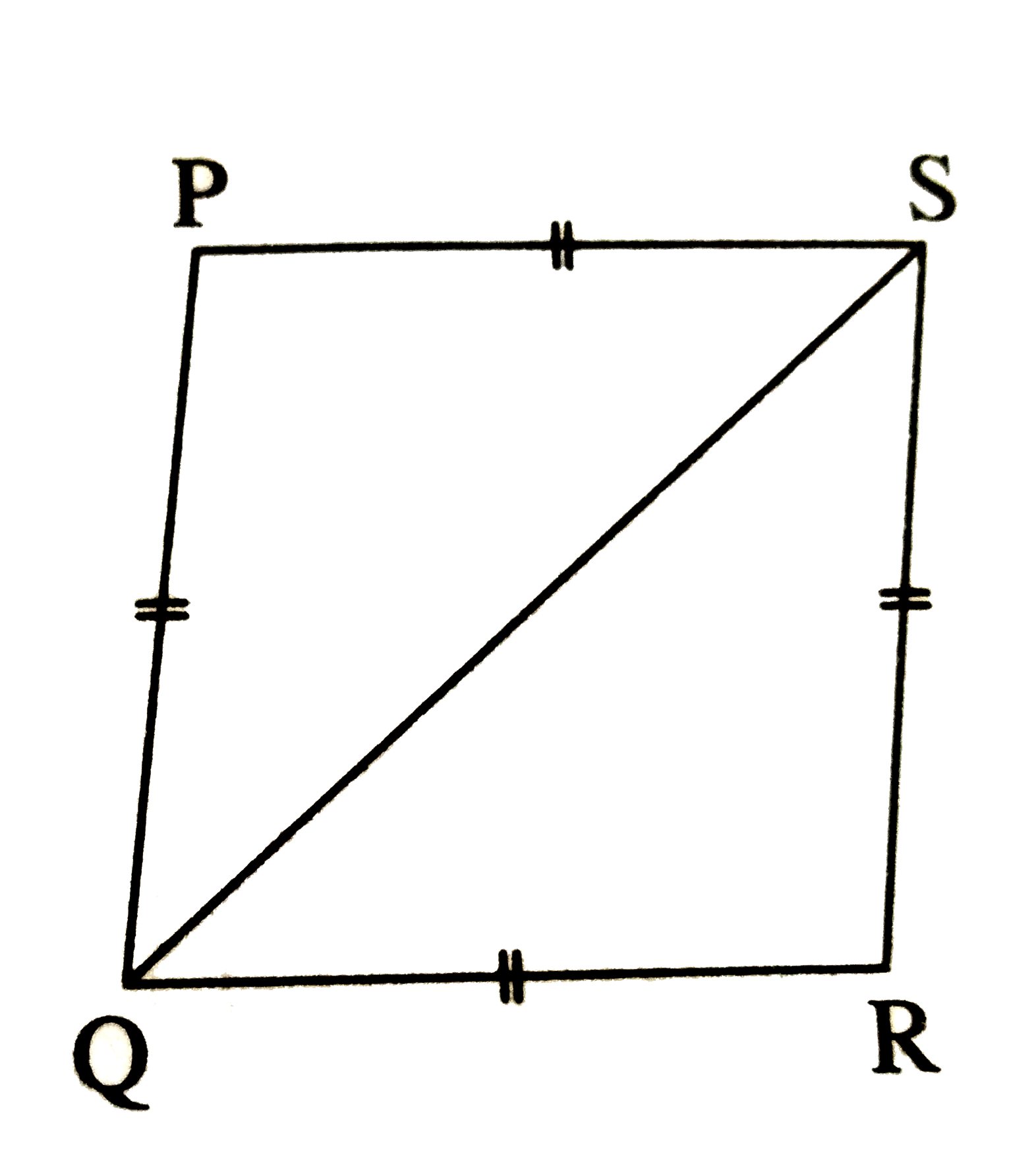
PQRS is rhombus with ∠QPS=50∘. Find ∠PQS.
The correct Answer is:65∘
To find the angle ∠PQS in the rhombus PQRS where ∠QPS=50∘, we can follow these steps:
Step 1: Understand the properties of a rhombus
In a rhombus, opposite angles are equal, and the diagonals bisect each other at right angles (90 degrees).
Step 2: Identify the angles
Given that ∠QPS=50∘, we can denote:
- ∠QPS=50∘
- Since opposite angles are equal in a rhombus, ∠PSQ=50∘ as well.
Step 3: Use the property of diagonals
Let the diagonals intersect at point O. The diagonals bisect the angles of the rhombus. Thus:
- ∠POQ=12∠QPS=12×50∘=25∘
Step 4: Analyze triangle POQ
In triangle POQ, we know:
- ∠POQ=25∘
- ∠OPQ=∠PQS (since PQ=PS in a rhombus)
Step 5: Apply the triangle sum property
The sum of angles in triangle POQ is:
∠POQ+∠OPQ+∠PQO=180∘
Substituting the known values:
25∘+∠PQS+∠PQO=180∘
Since ∠PQO=∠PQS, we can denote ∠PQS as x:
25∘+x+x=180∘
This simplifies to:
25∘+2x=180∘
Step 6: Solve for x
Subtract 25∘ from both sides:
2x=180∘−25∘
2x=155∘
Now divide by 2:
x=155∘2=77.5∘
Conclusion
Thus, ∠PQS=77.5∘.
In a rhombus, opposite angles are equal, and the diagonals bisect each other at right angles (90 degrees).
Given that ∠QPS=50∘, we can denote:
- ∠QPS=50∘
- Since opposite angles are equal in a rhombus, ∠PSQ=50∘ as well.
Let the diagonals intersect at point O. The diagonals bisect the angles of the rhombus. Thus:
- ∠POQ=12∠QPS=12×50∘=25∘
In triangle POQ, we know:
- ∠POQ=25∘
- ∠OPQ=∠PQS (since PQ=PS in a rhombus)
The sum of angles in triangle POQ is:
∠POQ+∠OPQ+∠PQO=180∘
Substituting the known values:
25∘+∠PQS+∠PQO=180∘
Since ∠PQO=∠PQS, we can denote ∠PQS as x:
25∘+x+x=180∘
This simplifies to:
25∘+2x=180∘
Subtract 25∘ from both sides:
2x=180∘−25∘
2x=155∘
Now divide by 2:
x=155∘2=77.5∘
Thus, ∠PQS=77.5∘.
Topper's Solved these Questions
- QUARILATERAL BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - QUARILATERAL EXERCISE - PART-A( True (T) and False (F))
6 Videos
- QUARILATERAL BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - QUARILATERAL EXERCISE - Part - B
12 Videos
- PROBABILITY MIND MAPBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PROBABILITY MIND MAPEXERCISE - PRACTICE TEST
6 Videos
- STATISTICSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STATISTICSEXERCISE - PRACTICE TEST
5 Videos
Similar Questions
Knowledge Check
If PQRS is a rhombus and ∠SPQ=50∘, then ∠RSO is
A75∘B45∘C55∘D55∘ABCD is a rhombus such that ∠ACB=40∘. Find ∠ADB.
A20∘B30∘C50∘D40∘PQRS is a rhombus in which ∠R = 60°. Then PR : QS =
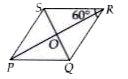 A√3 : 1B√3:√2C3 : 1D3 : 1
A√3 : 1B√3:√2C3 : 1D3 : 1
The given figure shows a rhombus ABCD in which angle BCD=80∘. Find angles xandy.
View SolutionIn the adjoining figure, ABCD is a rhombus. If ∠A=70∘, find ∠CDB.

View Solution
In the figure above, PQRS is a square , ∠PTR=110∘, then find ∠TPS.
View SolutionABCD is a rhombus such that ∠ACB=50∘. Then. ∠ADB= ?
View SolutionPQRS is a parallelogram , if ∠PQS=40∘andPS=QS , then ∠SQR−∠QRS = ___________.
View Solution