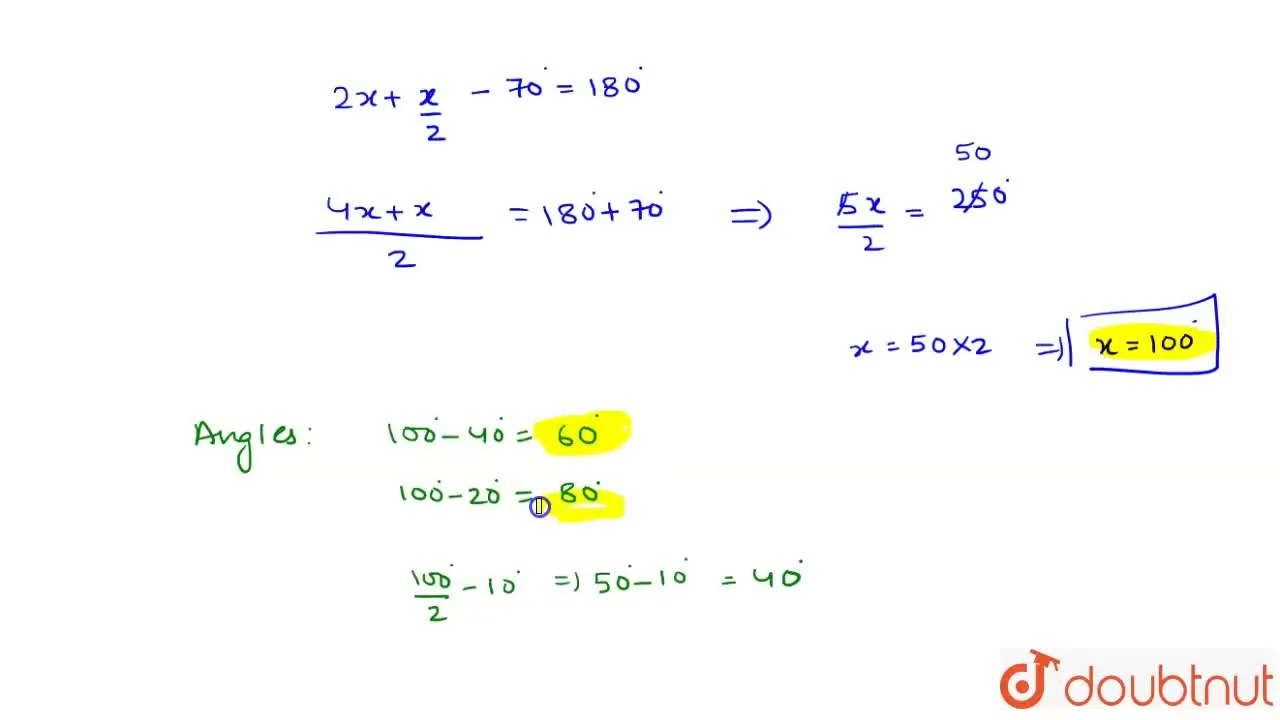The angles of a triangle are (x−40∘),(x−20∘),(x2−10∘) .Find the value of x & then find the angles of the triangle.
The correct Answer is:x=100∘,60∘,80∘,40∘
Step by step video, text & image solution for The angles of a triangle are (x-40^@),(x-20^@),(x/2-10^@) .Find the value of x & then find the angles of the triangle. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Related Playlists
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINES AND ANGLESEXERCISE - PART-C16videos
LINES AND ANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINES AND ANGLESEXERCISE - PART-D8videos
LINES AND ANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINES AND ANGLESEXERCISE - PRACTICE TEST8videos
LINES AND ANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - PRACTICE TEST12videos
LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - NUMBER SYSTEMSEXERCISE - Part - D18videos
NUMBER SYSTEMS
Similar Questions
Find the value of x in the given triangle
View SolutionFind the value of x from the given triangle
View SolutionThe angles of a triangle are (x−40)0, (x−20)0 and (12x−10)0. find the value of x.
View SolutionAngles of a triangle are (3x)∘,(2x−7)and(4x−11)∘ . Find the measure of x and each angle of the triangle
View SolutionThe angles of a triangle are 3x∘, (2x−7)∘and (4x−11)∘. The value of x is
View SolutionThe angles of a triangle are 40∘,60∘and80∘. Find the ratio of the angles in the same order of the triangle .
View SolutionThe angles of a triangle are (3x)0(2x−7)0and(4x−11)0. The value of x is
View SolutionThe angles of a quadrilateral are (x+20,(x−20),(2x+5),(2x−5). Find the value of x.
View Solutionthe measure of angles of triangle are x∘,(x−20)∘,(x−40)∘ find the measure of each angle
View SolutionThe angles of a triangle are (3x)∘, (2x−7)∘ and (4x−11)∘. Then, x = ?
View Solution