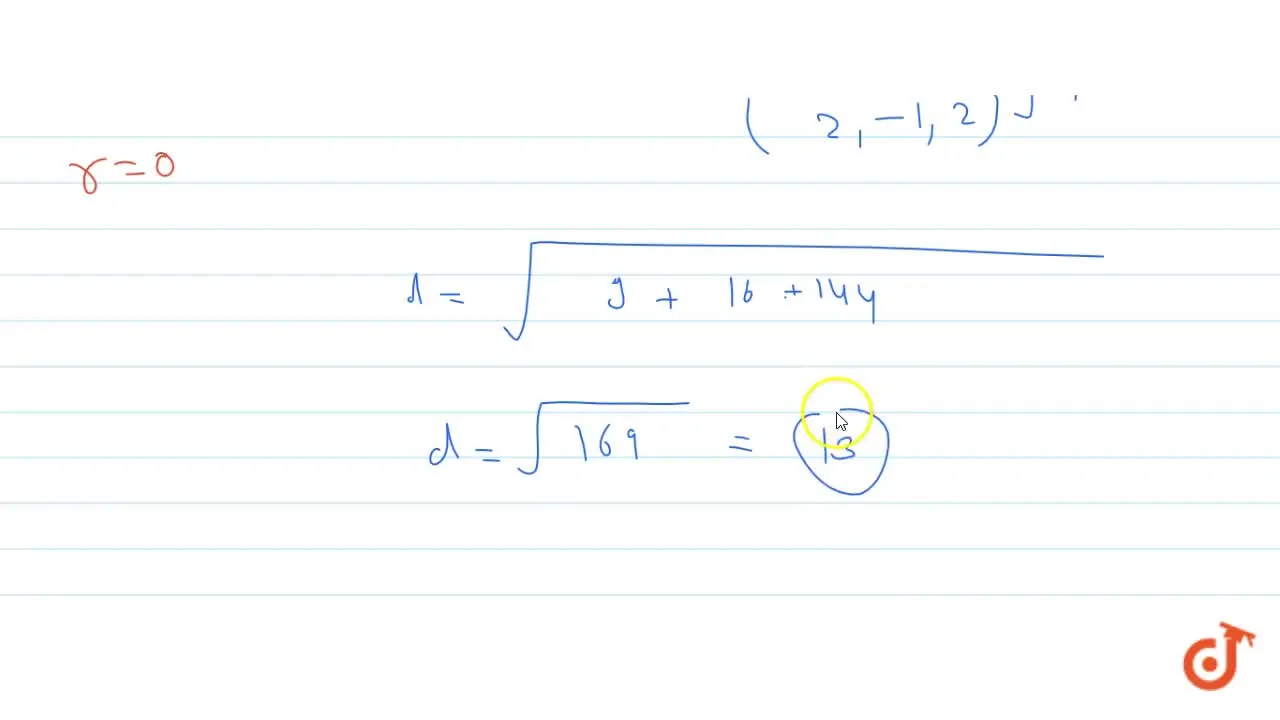Find the distance between the point with position vector ˆi−5ˆj−10ˆk and the point of intersection of the line x−23=y+14=z−212 with the plane x−y+z=5.
The equation of the given line is
r=(2i−j+2k)+λ(3i+4j+2k).....(1)
The equation of the given plane is
r.(i−j+k)=5........(2)
putting value of r
in equation (2), we get,
[(2i−j+2k)+λ(3i+4j+2k)[i−j+k]=5
⇒[(2+3λ)i+(4λ−1)j+(2+2λ)k][i−j+k]=5
⇒(2+3λ)−(4λ−1)+(2λ+2)=5
⇒λ=0
Thus the point of intersection of the given
line and the plane is,
r=2i−j+2k=(2,−1,2)
Hence, distance d between the points (2,−1,2) and
(−1,−5,−10) is
d=√(−1−2)2+(−5+1)2+(−10−2)2
=√9+16+144
=√169
=13
Related Playlists
Similar Questions
Find the distance between the point with position vector ˆi−5ˆj−10ˆk and the point of intersection of the line x−23=y+14=z−212 with the plane x−y+z=5.
View SolutionFind the distance between the points AandB with position vectors ˆi−ˆjand2ˆi+ˆj+2ˆk.
View SolutionFind the distance of the point with position vector −ˆi−5ˆj−10ˆk from the point of intersection of the line →r=(2ˆi−ˆj+2ˆk)+λ(3ˆi+4ˆj+12ˆk) with the plane →r.(ˆi−ˆj+ˆk)=5.
View SolutionFind the image of the point with position vector (3ˆi+ˆj+2ˆk) in the plane →r.(2ˆi−ˆj+ˆk)=4.
View SolutionFind the image of the point having position vector ˆi+2ˆj+4ˆk in the plane →r.2ˆi−ˆj+ˆk+3=0.
View SolutionShow that the points whose position vectors are 5ˆi+5ˆk, 2ˆi+ˆj+3ˆk and −4ˆi+3ˆj−ˆk are collinear
View SolutionThe image of the point with position vector ˆi+3ˆk in the plane r⋅(ˆi+ˆj+ˆk)=1 is
View SolutionThe angle between (ˆi+ˆj+ˆk) and line of the intersection of the plane 2x+y+4z=0 and 3x+4y+z=0 is
View SolutionFind the distance of the point 2ˆi−ˆj−4ˆk from the plane →r.(3ˆi−4ˆj+12ˆk)−9=0.
View SolutionPoints A and B have position vectors (5ˆi−2ˆj+4ˆk) and (ˆi+3ˆj−7ˆk) then find ∣∣∣−−→AB∣∣∣
View Solution