Three vectors of magnitude a,2a,3a meet in a point and their directions are along the diagonals of the adjacent faces of a cube. Determine their resultant.
To determine the resultant of three vectors of magnitudes a, 2a, and 3a that meet at a point and are directed along the diagonals of adjacent faces of a cube, we can follow these steps:
Step 1: Define the Vectors
We need to visualize the cube and define the vectors based on their directions. The three vectors can be defined as follows:
- Let →p be the vector of magnitude a along the diagonal of the face in the x-z plane.
- Let →q be the vector of magnitude 2a along the diagonal of the face in the y-z plane.
- Let →r be the vector of magnitude 3a along the diagonal of the face in the x-y plane.
Step 2: Express the Vectors in Component Form
Using the fact that these vectors make angles of 45∘ with the axes, we can express them in terms of unit vectors ^i, ^j, and ^k:
- For →p:
→p=a(cos45∘^i+cos45∘^k)=a(1√2^i+1√2^k)=a√2^i+a√2^k
- For →q:
→q=2a(cos45∘^j+cos45∘^k)=2a(1√2^j+1√2^k)=2a√2^j+2a√2^k
- For →r:
→r=3a(cos45∘^i+cos45∘^j)=3a(1√2^i+1√2^j)=3a√2^i+3a√2^j
Step 3: Calculate the Resultant Vector
Now, we can find the resultant vector →R=→p+→q+→r:
→R=(a√2+3a√2)^i+(2a√2)^j+(a√2+2a√2)^k
→R=4a√2^i+2a√2^j+3a√2^k
Step 4: Simplify the Resultant Vector
We can factor out a√2:
→R=a√2(4^i+2^j+3^k)
Step 5: Calculate the Magnitude of the Resultant Vector
The magnitude of the resultant vector →R is given by:
|→R|=∣∣∣a√2∣∣∣√(4)2+(2)2+(3)2
=a√2√16+4+9=a√2√29
=a√29√2=a√582
Final Result
Thus, the magnitude of the resultant vector is:
|→R|=a√582
We need to visualize the cube and define the vectors based on their directions. The three vectors can be defined as follows:
- Let →p be the vector of magnitude a along the diagonal of the face in the x-z plane.
- Let →q be the vector of magnitude 2a along the diagonal of the face in the y-z plane.
- Let →r be the vector of magnitude 3a along the diagonal of the face in the x-y plane.
Using the fact that these vectors make angles of 45∘ with the axes, we can express them in terms of unit vectors ^i, ^j, and ^k:
- For →p:
→p=a(cos45∘^i+cos45∘^k)=a(1√2^i+1√2^k)=a√2^i+a√2^k
→q=2a(cos45∘^j+cos45∘^k)=2a(1√2^j+1√2^k)=2a√2^j+2a√2^k
→r=3a(cos45∘^i+cos45∘^j)=3a(1√2^i+1√2^j)=3a√2^i+3a√2^j
Now, we can find the resultant vector →R=→p+→q+→r:
→R=(a√2+3a√2)^i+(2a√2)^j+(a√2+2a√2)^k
→R=4a√2^i+2a√2^j+3a√2^k
We can factor out a√2:
→R=a√2(4^i+2^j+3^k)
The magnitude of the resultant vector →R is given by:
|→R|=∣∣∣a√2∣∣∣√(4)2+(2)2+(3)2
=a√2√16+4+9=a√2√29
=a√29√2=a√582
Thus, the magnitude of the resultant vector is:
|→R|=a√582
Topper's Solved these Questions
Similar Questions
Three coinitial vectors of magnitudes a, 2a and 3a meet at a point and their directions are along the diagonals if three adjacent faces if a cube. Determined their resultant R. Also prove that the sum of the three vectors determinate by the diagonals of three adjacent faces of a cube passing through the same corner, the vectors being directed from the corner, is twice the vector determined by the diagonal of the cube.
View SolutionTwo vectors of equal magnitude are acting through a point. The magnitude of resultant is equal to the magnitude of either vectoe. Find the angle between the vectors.
View Solution
Knowledge Check
Three forces of magnitudes 1,2, and 3 dynes meet in a point and act along diagonals of three adjacent faces of a cube.The resultant force is
A114 dyneB6 dynesC5 dynesDnone of the abiveThree forces of magnitudes 1,2, and 3 dynes meet in a point and act along diagonals of three adjacent faces of a cube.The resultant force is
A114 dyneB6 dynesC5 dynesDnone of the abiveTwo vectors of magnitude 4 and 6 are acting through a point. If the magnitude of the resultant is R
A4<R<6B4<R<10C2≤R≤10D2≥R≥10
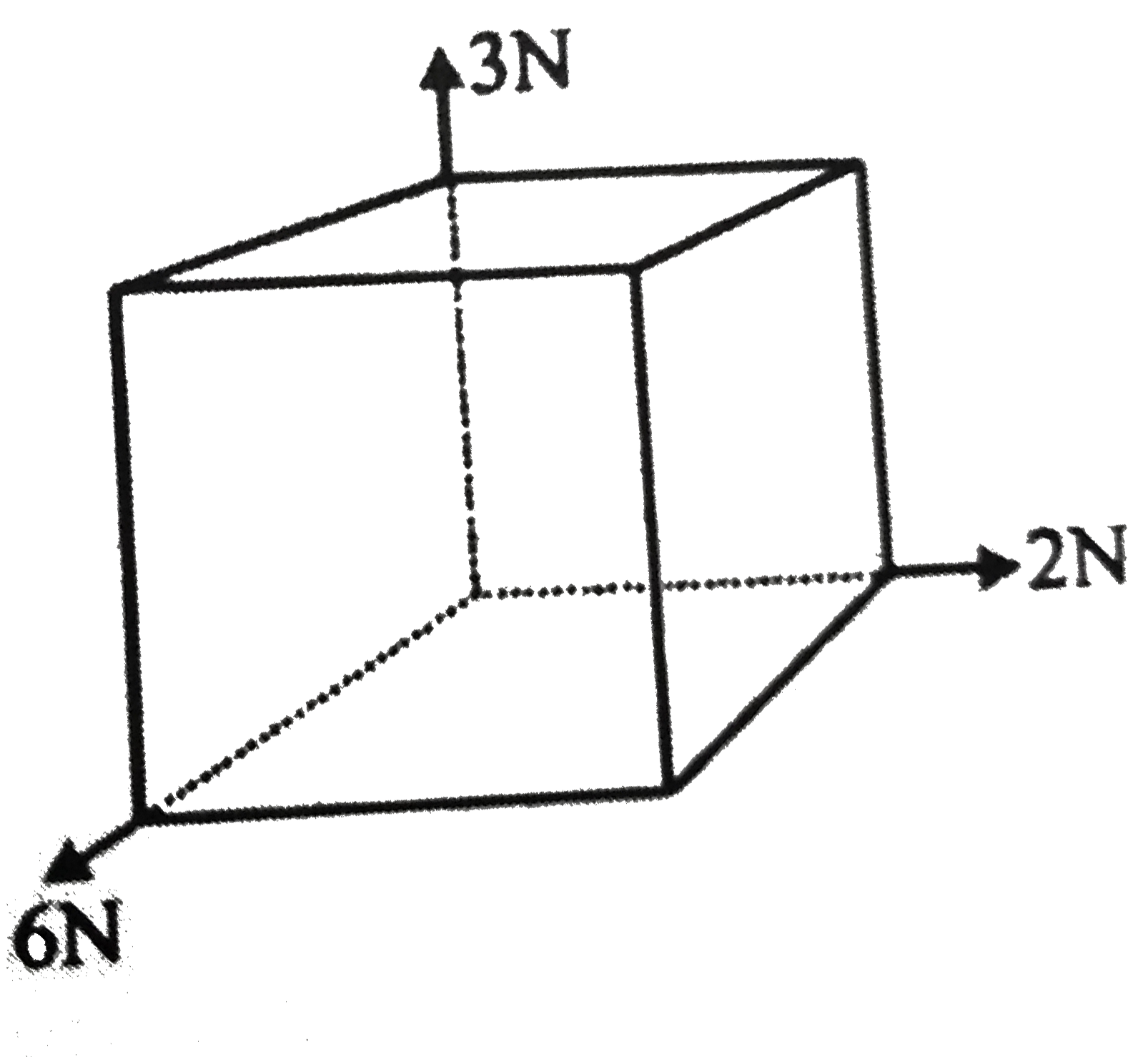
Three forces of magnitudes 2N, 3N and 6N act at corners of a cube along three sides as shown in figure. Find the resultant of these forces in N.
View SolutionTwo vectors having equal magnitudes A make an angle θ with eahc other. Find the magnitude and direction of the resultant.
View SolutionThree vector each of magnitude A are acting at a point such that angle between any two consecuitve vectors in same plane is 60∘ The magniude of their resultant is
View SolutionThree are N coplancar vectors each of magnitude V Each vector is inclined to the preceding vector atangle 2πN What is the magnitude of their resultant ?
View SolutionThe direction of three forces 1N, 2N and 3N acting at a point,are parallel to the sides of an equilateral triangle taken in order. The magnitude of their resultant is:
View Solution