A producer has 20 and 10 unit of labour and capital respectively which he can use to produce two kinds of goods X and Y. To produce one unit of x, 2 units of capital and 1 unit of labour is required. To produce one unit of Y,3 of labour and 1 unit of capital is required. If X and Y are priced at Rs. 80 and Rs. 100 per unit respectively, how should the producer use his resources to maximise the total revenue?
The correct Answer is:At 25 km/h he should travel 50/3, at 40 km/h 40/3 km. Maximum distance 30 km in 1 hr.
To solve the problem of maximizing the total revenue for the producer using linear programming, we will follow these steps:
Step 1: Define the Variables
Let:
- x = number of units of good X produced
- y = number of units of good Y produced
Step 2: Formulate the Constraints
From the problem, we know the following about the resources required for production:
- To produce one unit of good X, 2 units of capital and 1 unit of labor are required.
- To produce one unit of good Y, 1 unit of capital and 3 units of labor are required.
Given the total resources available:
- Total labor available = 20 units
- Total capital available = 10 units
We can formulate the constraints based on these requirements:
1. Labor Constraint:
1x+3y≤20
2. Capital Constraint:
2x+1y≤10
3. Non-negativity Constraints:
x≥0,y≥0
Step 3: Formulate the Objective Function
The objective is to maximize the total revenue, which can be expressed as:
Z=80x+100y
where 80 and 100 are the prices of goods X and Y respectively.
Step 4: Graph the Constraints
To graph the constraints, we can convert the inequalities into equations to find the intercepts.
1. For the labor constraint x+3y=20:
- When x=0, y=203≈6.67
- When y=0, x=20
2. For the capital constraint 2x+y=10:
- When x=0, y=10
- When y=0, x=5
Step 5: Identify the Feasible Region
Plot the lines on a graph and shade the feasible region that satisfies both constraints along with the non-negativity constraints. The feasible region will be bounded by the axes and the lines.
Step 6: Find the Corner Points
The corner points of the feasible region can be found by solving the equations of the lines:
1. Intersection of x+3y=20 and 2x+y=10:
- Solve the equations simultaneously to find the intersection point.
2. The other corner points will be the intercepts:
- (0,0)
- (0,10)
- (5,0)
- Intersection point found above.
Step 7: Evaluate the Objective Function at Each Corner Point
Calculate Z at each corner point:
1. Z(0,0)=80(0)+100(0)=0
2. Z(0,10)=80(0)+100(10)=1000
3. Z(5,0)=80(5)+100(0)=400
4. Z at the intersection point (let's say it is (xc,yc)).
Step 8: Determine the Maximum Revenue
Compare the values of Z calculated at the corner points. The maximum value will indicate the optimal production levels of goods X and Y.
Final Answer
The producer should produce the quantities of goods X and Y that correspond to the corner point yielding the maximum revenue.
Let:
- x = number of units of good X produced
- y = number of units of good Y produced
From the problem, we know the following about the resources required for production:
- To produce one unit of good X, 2 units of capital and 1 unit of labor are required.
- To produce one unit of good Y, 1 unit of capital and 3 units of labor are required.
- Total labor available = 20 units
- Total capital available = 10 units
1. Labor Constraint:
1x+3y≤20
2. Capital Constraint:
2x+1y≤10
3. Non-negativity Constraints:
x≥0,y≥0
The objective is to maximize the total revenue, which can be expressed as:
Z=80x+100y
where 80 and 100 are the prices of goods X and Y respectively.
To graph the constraints, we can convert the inequalities into equations to find the intercepts.
- When x=0, y=203≈6.67
- When y=0, x=20
- When x=0, y=10
- When y=0, x=5
Plot the lines on a graph and shade the feasible region that satisfies both constraints along with the non-negativity constraints. The feasible region will be bounded by the axes and the lines.
The corner points of the feasible region can be found by solving the equations of the lines:
1. Intersection of x+3y=20 and 2x+y=10:
- Solve the equations simultaneously to find the intersection point.
- (0,0)
- (0,10)
- (5,0)
- Intersection point found above.
Calculate Z at each corner point:
1. Z(0,0)=80(0)+100(0)=0
2. Z(0,10)=80(0)+100(10)=1000
3. Z(5,0)=80(5)+100(0)=400
4. Z at the intersection point (let's say it is (xc,yc)).
Compare the values of Z calculated at the corner points. The maximum value will indicate the optimal production levels of goods X and Y.
The producer should produce the quantities of goods X and Y that correspond to the corner point yielding the maximum revenue.
Topper's Solved these Questions
- LINEAR PROGRAMMING BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINEAR PROGRAMMING EXERCISE - ONE MARKS QUESTIONS
8 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - 4 MARK QUESTIONS
31 Videos
- MATRICES AND DETERMINANTSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - MATRICES AND DETERMINANTSEXERCISE - SIX MARK QUESTIONS
20 Videos
Similar Questions
(Manufacturing Problem) A manufacturer considers that men and women workers are equally efficient and so he pays tehm at the same rate.He has 30 and 17 units of workers(male and femlae) and capital respectively, which he uses to produce two types of goods A and B.To produe one unit of A, 2 workers and 3 units of capital are required whie 3 workers and 1 unit of capital are required to produce one unit of B. If A and B are priced at ₹. 100 and₹.120 per unit respectively, how should he use his resources to maximise the total revenue?Form the above as an LPP and solve graphically.
View SolutionFour units of labour produce 100 unit of output and 5 units of labour produce 120 units of output. Calculate MP of the labour.
View Solution
Knowledge Check
Product per unit of labour employed is termed as :
AAverage productBMarginal productCTotal productDNone of theseA company produces three products. The products are processed on 3 different machines. The time required to manufacture one unit of each the three products and the daily capacity of three machines are given in the table below :

How many units of product 1 can be produced in one day?A160B205C225D64
Four units of labour produce 1000 units of output and 5 units of labour produce 1200 units of output. Calculate MP of the labour.
View SolutionIndia is a labour abundance and capital scarce economy. Which technique of production should be used to produce the commodity?
View SolutionA farm is engaged in breeding pigs. The pigs are fed on various products grown on the farm. To ensure certain nutrient constituents X,Y and Z, It is necessary to mix two types of feeds A and B . One unit of product A contains 36 units of X, 3 units of Y and 20 units of Z. One unit of product B contains 6 units of X, 12 units of Y and 10 units of Z. The minimum requirement of X,Y and Z is 108 units, 36 units and 100 units respectively. Product A costs Rs. 20/unit and product B costs Rs 40/unit. Formulate this problem sa a linear programming problem to minimize the total cost.
View SolutionA producer can sell any quantity of a commodity at a given price of Rs. 10 per unit. His cost schedule is given below:
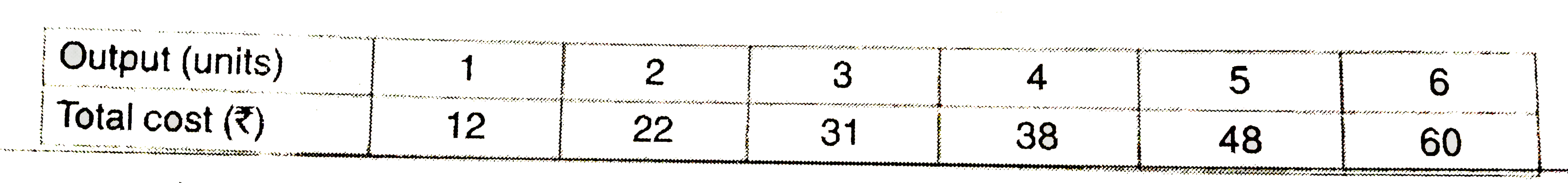
How many units should he produce to get maximum profit ? Explain.
View Solution4 units of a factor of production produce 100 units of output, and 5 units produce 120 units of output, Calculate MP of that factor.
View SolutionA consumer consumers only two goods X and Y whose prices are Rs 5 and Rs 4 per unit respectively. If MUY=16 at the point of consumer's equilibrium, calculate MUX.
View Solution
