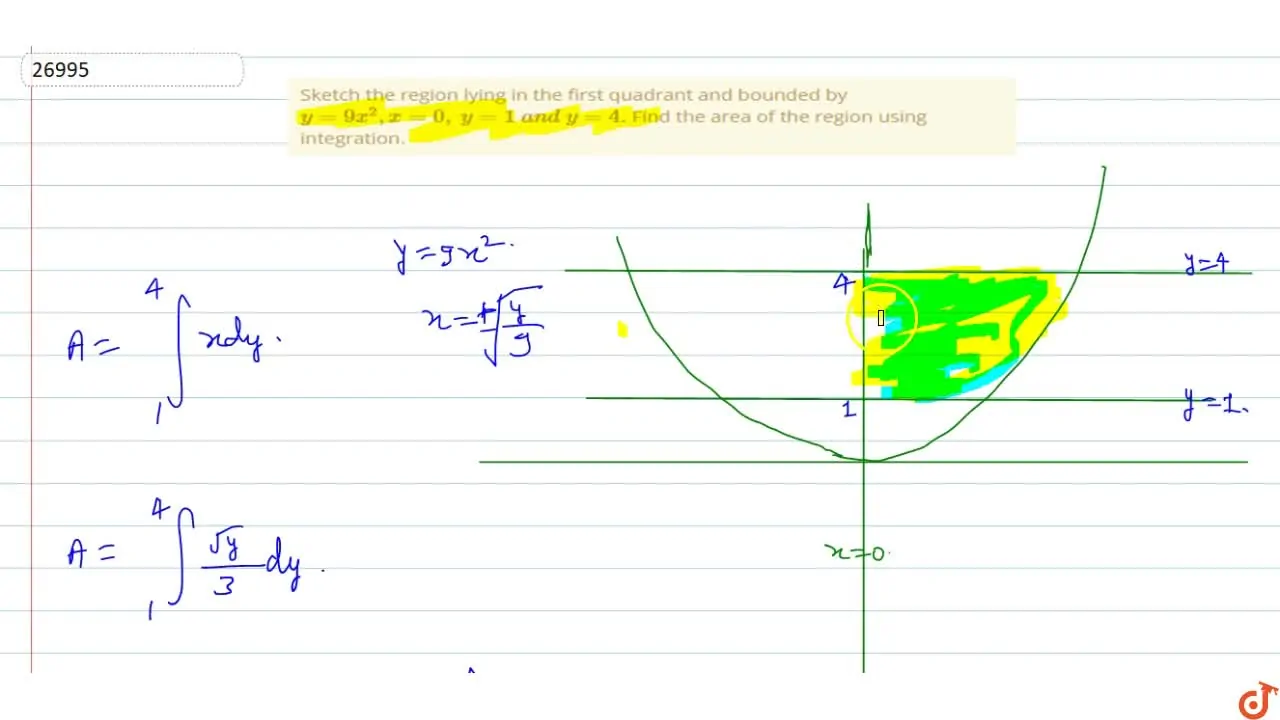
Sketch the region lying in the first quadrant and bounded by $y = 9 x^{2}, x = 0, y = 1 a n d y = 4 .$ Find the area of the region using integration.

Video Solution

Text Solution

Verified by Experts

Here, $x^{2} = \frac{y}{9}$ is a upward parabola having its vertex at the origin and $y = 1, y = 4$ are the lines which are parallel to ${x}$ -axis at ${y} = 1$ to ${y} = 4$ unit distance from it Similarly $x^{2} = \frac{y}{9}$ has even power of $y$ and is symmetrical about $y -$ axis So the required area is written as

Required area $= \int_{1}^{4} {x d y}$

$= \int_{1}^{4} \frac{\sqrt{y}}{3} d y$

$= \frac{1}{3} {⎡ ⎢ ⎣ \frac{y^{\frac{3}{2}}}{\frac{3}{2}} ⎤ ⎥ ⎦}_{1}^{4}$

$= \frac{2}{9} [4^{\frac{3}{2}} - 1^{\frac{3}{2}}]$

$= \frac{2}{9} (8 - 1)$

$= \frac{14}{9} sq. units.$

Updated on:21/07/2023

Area lying in the first quadrant and bounded by the circle $x^{2} + y^{2} = 4$ and the lines $x = 0 and x = 2$ is
A $π$
B $\frac{π}{2}$
C $\frac{π}{3}$
D $\frac{π}{4} .$
Area lying in the first quadrant and bounded by the circle $x^{2} + y^{2} = 4$ and the lines $x = 0 and x = 2$ is :
A $π$
B $\frac{π}{2}$
C $\frac{π}{2}$
D $\frac{π}{4}$
The area (in sq. units) of the region in the first quadrant bounded by $y = x^{2}, y = 2 x + 3$ and the y - axis is
A $2 \sqrt{3}$
B6
C9
D $\frac{44}{3}$