A beam is supported at the two ends and is uniformly loaded. The bending moment M at a distance x from one end is given by M=WL2x−W2x2 M=Wx3−W3x3L2 Find the point at which M is maximum in each case.
M=WL2x−W2x2
On differentiation , we get,
{dM}{dx}={WL}2−2{W}2{x}
equate, {dM}{dx}=0
⇒WL2−2W2x=0
WL2=2W2 x
{x}={L}2
{d}2{M}d{x}2=−2{W}2=−{W}<0
Therefore, f(x) is maximum when x=L2
Topper's Solved these Questions
Similar Questions
A beam is supported at the two ends and is uniformly loaded. The bending moment M at a distance x from one end is given by M=WL2×−W2x2 Find the point at which M is maximum in each case.
View SolutionA beam is supported at the two ends and is uniformly loaded. The bending moment M at a distance x from one end is given by M=Wx3−W3x3L2 . Find the point at which M is maximum.
View Solution
Knowledge Check
A rocket in a fireworks display explodes high in the air. The sound spreads out uniformly in all directions. The intensity of the sound is 2.0×10W/m2 at a distance of 120 m from the explosion. Find the distance from the source at which the intensity is 0.80×10−6W/m2 .
A690 mB220 mC110 mD190mA rod of mass m and length L , pivoted at one of its ends, is hanging vertically . A bullet of the same mass moving at speed v strikes the rod horizontally a a distance x from its pivoted end and gets embedded in it. The combined system now rolates with rotates with angular speed ω about the pivot . The maximum angular speed ωM is achieved for x=xm . Then .
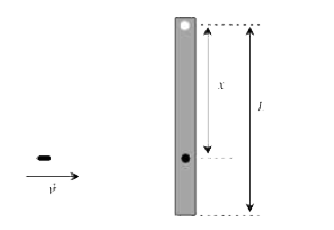 Aω=3vxL2+3x2Bω=12vxL2+12x2CxM=1√3DωM=v2L√3
Aω=3vxL2+3x2Bω=12vxL2+12x2CxM=1√3DωM=v2L√3
A beam is supported at the two ends and is uniformly loaded. The bending moment M at a distance x from one end is given by M=WL2x−W2x2 . Find the point at which M is maximum.
View SolutionA beam of length l is supported at one end. If W is the uniform load per unit length, the bending moment M at a distance x from the end is given by M=12lx−12Wx2. Find the point on the beam at which the bending moment has the maximum value.
View SolutionA beam of weight W supports a block of weight W. The length of the beam is I. and weight is at a distance L4 from the left end of the beam. The beam rests on two rigid supports at its ends. Find the reactions of the supports.

View SolutionThe electric field in an electromagnetic wave is given by: E=(50NC−1)sinω(t−xc)F∈dthe∫ensity(∈W/m^2 ) of the wave.
View SolutionThe maximum intensity in the case of n identical waves each of intensity 2Wm2is32Wm2 the value of n is
View SolutionOne end of a horizontal uniform beam of weight W and length L is hinged on a vertical wall at point O and its other end is supported by a light inextensible rope. The other end of the rope is fixed at point Q at a height L above the hinge at point O. A block of weight αW is attached at the point Q at a height L above the hinge at point O. A block of weight αW is attached at the point P of the beam as shown in the figure. The rope can sustain a maximum tension of 2(√2)W. Which of the following statements is/are correct?
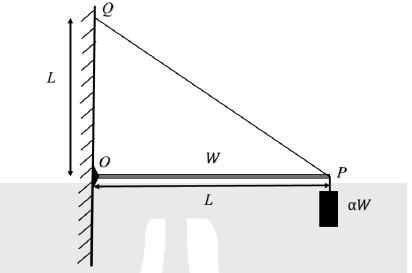
View Solution